Notes: Jekyll 对Latex公式渲染的效果一般,这个笔记可能会存在公式渲染错误的情况。最好的阅读方式clone整个blog到本地,然后用Typora打开_post文件夹下的md源文件来阅读。
1. 朴素贝叶斯法
1.1. 问题设定
给定训练集 $T={\left(x_{1}, y_{1}\right),\left(x_{2}, y_{2}\right), …, \left(x_{n}, y_{n}\right)}$ 由 $P(X, Y)$ 独立同分布产生1。朴素贝叶斯法的目的就是习得 $P(X, Y)$.
独立是指 $x_1, x_2, …, x_n$取值不影响,同分布指的是训练集由同一个数据集产生。
1.2. 方法
学习先验概率分布的极大似然 $P(Y = c_k)$ 及条件概率分布 $P(X=x \mid Y=c_k)$ 的极大似然,从而学习到联合概率分布 $P(X, Y)$ 的极大似然。
需要注意的是,朴素贝叶斯法对条件概率分布做了条件独立性的假设,也就是训练数据的各个维度的分量相互独立。这是一个较强的假设。具体地,条件独立性的假设是: \(\begin{array}{l} P\left(X=x \mid Y=c_{k}\right) \\ =P\left(X^{(1)}=x^{(1)}, X^{(2)}=x^{(2)}, \ldots, X^{(n)}=x^{(n)} \mid Y=c_{k}\right) \\ =\prod_{j=1}^{n} P\left(X^{(j)}=x^{(j)} \mid Y=c_{k}\right) \end{array}\) 朴素贝叶斯法做分类的时候,对给定的输入 $x$,通过学习到的模型计算后验概率分布 $P(Y=c_k|X=x)$,将后验概率最大的类作为分类结果。根据贝叶斯定律,后验概率可通过: \(P\left(Y=c_{k} \mid X=x\right)=\frac{P\left(X=x \mid Y=c_{k}\right) P\left(Y=c_{k}\right)}{\sum_{k} P\left(X=x \mid Y=c_{k}\right) P\left(Y=c_{k}\right)}\) 计算可得。计算过程中需要把(1)代入(2)中,计算每个 $x$ 中每个feature的每个取值在每个 $y$ 上的统计概率,可见计算量非常大。
1.3. 贝叶斯估计
在计算条件概率 $P\left(X^{(j)}=a_{jl} \mid Y=c_{k}\right)$ 的时候可能会出现概率值为0的情况,其中 $l=1,2, \ldots, n(l), \quad k=1,2, \ldots, K$。$a_{jl}$ 是 $X^{(j)}$ 可能的取值之一。$l$ 共有 $n(l)$种不同的取值,所有$a_{jl}$表示在第 $j$ 个特征上共有 $n(l)$ 种不同的取值。显然,概率值为0会影响到后验概率的计算结果。我们用贝叶斯估计来解决这个问题。具体地,条件概率的贝叶斯估计是: \(P_{\lambda}\left(X^{(j)}=a_{j l} \mid Y=c_{k}\right)=\frac{\sum_{i=1}^{N} I\left(x_{i}^{(j)}=a_{j l}, y_{i}=c_{k}\right)+\lambda}{\sum_{i=1}^{N} I\left(y_{i}=c_{k}\right)+n(l) \lambda}\) 其中,$N$ 是总的样本数,$\lambda \geq 0$。当 $\lambda = 0$ 的时候,称为极大似然估计。常取 $\lambda = 1$,此时称为拉普拉斯平滑。显然,对于任何 $l,k$,有: \(P_{\lambda}\left(X^{(j)}=a_{j l} \mid Y=c_{k}\right)>0\) 和 \(\sum_{l=1}^{S_{j}} P_{\lambda}\left(X^{(j)}=a_{j l} \mid Y=c_{k}\right)=1\) 同样的,先验概率的贝叶斯估计为: \(P_{\lambda}\left(Y=c_{k}\right)=\frac{\sum_{i=1}^{N} I\left(y_{i}=c_{k}\right)+\lambda}{N+K \lambda}\)
某程度上,这个方法能够判断训练集上没出现过的类别。但是当然啦,前提是你得知道这个类别的存在。
2. EM算法
2.1. 问题设定
首先需要从整体上理解一下EM算法是干什么用的。如果概率模型的变量都是观测变量,那么给定数据,可以用极大似然估计(也就是朴素贝叶斯法)或者贝叶斯估计法估计模型参数。但是,当模型含有隐变量,就不能简单的应用上述方法。EM算法就是用于含有隐变量的概率模型参数的极大似然估计法。
在无监督学习当中,给定训练集 $T={x^{(1)}, x^{(2)}, \ldots, x^{(m)}}$, 求生成 $T$ 的概率模型 $P(x, z)$,其中 $z$ 为隐含变量集合。一般会把 $z^{(i)}$理解为描述 $x^{(i)}$ 是来自哪个分模型的一个变量,取值范围是分模型的集合。所以我们的目的是最大化下面的似然函数: \(\begin{aligned} \ell(\theta) &=\sum_{i=1}^{m} \log p(x^{(i)} ; \theta)\\ &=\sum_{i=1}^{m} \log \sum_{z^{(i)}} p(x^{(i)}, z^{(i)} ; \theta)\\ &=\sum_{i=1}^{m} \log \sum_{z^{(i)}} p(x^{(i)} ; z^{(i)}, \theta) p(z^{(i)}) \end{aligned}\) 其中,$P$ 为已知模型或者说已知分布,但是参数未知,$\theta$ 为模型参数集合。如果 $z$ 是确定的(具体哪个样本来自于哪个分布),那么 log 里面的连加符号就可以去掉了,然后整个式子就可以通过求导来最优化。但是既然说了 $z$ 是隐藏变量,那我们肯定是不知道 $z$ 的,也就是说 $z$ 是不确定的,我们可以通过历史数据得到 $z$ 的先验分布,但是也就仅此而已,$z$ 仍然是不确定的。连加符号就是因为 $z$ 是不确定的,所以要把所有可能的 $z$ 算进去,就好像全概率公式那样,具体可以参考下面的GMM的例子。
试想一下,在$z$ 不确定的情况下,如果直接求导来最大化 $\ell(\theta)$ 的话,log里面还有多个+号,将导致无法求解。
2.2. Jensen 不等式
假设 $f$ 是domain为实数的函数。如果 $f^{‘’}(x) \geq 0$ 对于所有 $x \in R$ 成立,则 $f$ 是一个凸函数,如果$f^{‘’}(x) \leq 0$ , 则 $f$ 是一个凹函数。当 $f$ 的自变量是向量时,如果它的hessian矩阵是半正定的 ($H \geq 0$),则 $f$ 是凸函数。
定理: 如果 $f$ 是凸函数,设 $X$ 为变量,则 $E(f(X)) \geq f(EX)$ ,如下图。如果 $f$ 是凹函数,则$E(f(X)) \leq f(EX)$。
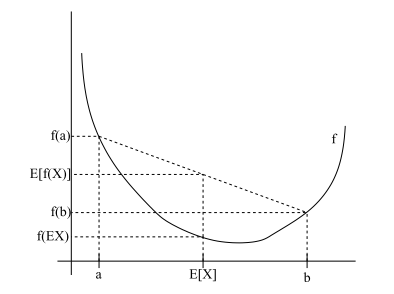
如果 $f$ 是严格凸函数($f^{‘’}(x) > 0$ ), 则当且仅当 $X = EX$, 也就是说 $X$ 为常数,我们有$E(f(X)) = f(EX)$ 。
2.3. EM
紧接着上面设定的无监督求概率分布的问题。因为隐藏变量 $z$ 的存在以及它的不确定性,所以极大化 $\ell(\theta)$ 会变得很困难。那么EM算法是怎么解决这个困难的呢?总的来说,EM算法可以细分成E步(expectation)和M步(maximum)。E步为 $\ell(\theta)$ 构建一个下界,这个下界相当于让$\ell(\theta)$ 在特定条件下有了新的表达形式(去掉了log里面的连加形式),然后M步就是通过求导来最大化这个下界。不断重复EM直至收敛。其实从另外一个角度来理解,E步可以说就是基于当前参数去估计一个 $z$ 的分布,这个分布很特殊,它的数学特性可以使得 $\ell(\theta)$ 等于其下界,从而有一个新的表达形式。
下面来看看E步是如何估计下界。首先,我们假设 $z^{(i)}$ 的某种分布函数是$Q$, 则我们有: \(Q(z^{(i)} = 任意一个可能的取值) \geq 0, \quad \sum_{z^{(i)}} Q(z^{(i)})=1\) 这里特别需要注意的一点是,目前为止,我们出现了2个描述 $z$ 的概率分布的形式,一个是出现在2.1小节里面的 $p\left(z^{(i)} \right)$ ,第二个是 $Q(z)$。前者我们可以认为是 $z$ 的先验分布。后者我们可以认为是 $z$ 的任意的一个可能的分布,这个分布是什么目前来说并不重要,它是什么都不影响下面这个公式的成立。
然后,考虑以下情形我们是怎么得出 $\ell(\theta)$ 的下界的: \(\begin{aligned} \ell(\theta) &= \sum_{i=1}^{m} \log p\left(x^{(i)} ; \theta\right) \\ &= \sum_{i=1}^{m} \log \sum_{z^{(i)}} p\left(x^{(i)}, z^{(i)} ; \theta\right) \\ &= \sum_{i=1}^{m} \log \sum_{z^{(i)}} Q\left(z^{(i)}\right) \frac{p\left(x^{(i)}, z^{(i)} ; \theta\right)}{Q\left(z^{(i)}\right)} \\ & \geq \sum_{i=1}^{m} \sum_{z^{(i)}} Q\left(z^{(i)}\right) \log \frac{p\left(x^{(i)}, z^{(i)} ; \theta\right)}{Q\left(z^{(i)}\right)} \end{aligned}\)
解释:
- 第1行到第2行就是一个全概率公式而已。
- 仔细观察上面公式,我们可以发现,第2行到第3行的变化是对 $p$ 的分子分母同时乘以 $Q\left(z^{(i)}\right)$。
- 显然,$\sum_{z^{(i)}} Q\left(z^{(i)}\right) \frac{p\left(x^{(i)}, z^{(i)} ; \theta\right)}{Q\left(z^{(i)}\right)}$ 是 $\frac{p\left(x^{(i)}, z^{(i)} ; \theta\right)}{Q\left(z^{(i)}\right)}$ 的期望值 (EX)。因为log是严格的凹函数 $f$,所以,由上面提到的Jensen不等式对严格凹函数有 $E(f(X)) \leq f(EX)$ 可得到第3行到第4行的转化。等号当且仅当 $X = EX$ 的时候成立。
对于任何的 $Q\left(z^{(i)}\right)$, 上面公式的第4行给出了 $\ell(\theta)$ 的下界。然而,$Q\left(z^{(i)}\right)$ 可能的分布有很多种,那么我们应该选哪一种呢?假设我们现在已经有了一些初始的 $\theta$ 值,显然我们希望在这个 $\theta$ 值的前提下,$\ell(\theta)$ 能够尽量贴近其下界,最好是令其等于下界。从而当递归进行EM的时候能够保证似然函数是递增的。
为了使 $\ell(\theta)$ 等于其下界,由Jensen不等式的性质可知,我们需要 $\frac{p\left(x^{(i)}, z^{(i)} ; \theta\right)}{Q\left(z^{(i)}\right)}$ 是一个不依赖于 $z^{(i)}$ 的常数 $c$。也就是: \(\frac{p\left(x^{(i)}, z^{(i)} ; \theta\right)}{Q\left(z^{(i)}\right)}=c\) 其实这就等价于 $p\left(x^{(i)}, z^{(i)} ; \theta\right)$ 正比于 $Q\left(z^{(i)}\right)$ 即可。
事实上,因为我们知道 $Q\left(z^{(i)}\right)$ 是一个分布,也就是 $\sum_{z^{(i)}} Q(z^{(i)})=1$。我们进一步得到: \(\sum_{z^{(i)}} p\left(x^{(i)}, z^{(i)} ; \theta\right)=\frac{\sum_{z^{(i)}} p\left(x^{(i)}, z^{(i)} ; \theta\right)}{\sum_{z^{(i)}} Q(z^{(i)})}=\frac{p\left(x^{(i)}, z^{(i)} ; \theta\right)}{Q\left(z^{(i)}\right)}=c\) 式(9)的证明很简单:多个等式分子分母相加不变,这里认为每个样例的概率比值都是 $c$。
所以,我们得到了如下关系: \(\begin{aligned} Q_{i}\left(z^{(i)}\right) &= \frac{p\left(x^{(i)}, z^{(i)} ; \theta\right)}{c} \\ &= \frac{p\left(x^{(i)}, z^{(i)} ; \theta\right)}{\sum_{z^{(i)}} p\left(x^{(i)}, z^{(i)} ; \theta\right)} \\ &= \frac{p\left(x^{(n)}, z^{(n)} ; \theta\right)}{p\left(x^{(i)} ; \theta\right)} \\ &= p\left(z^{(i)} \mid x^{(i)} ; \theta\right) \end{aligned}\) 至此,我们就得到 $Q\left(z^{(i)}\right)$ 等价于已知 $x^{(i)}$ 和当前 $\theta$ 的后验概率,可有已知量求得,用贝叶斯定理来求(需要有一个隐变量分布的先验数据),参考GMM的例子。也就是说,$Q\left(z^{(i)}\right)$ 是个常数。其实这一步是E步,建立 $\ell(\theta)$ 的下界。接下来的M步,就是在给定 $Q\left(z^{(i)}\right)$ 后,调整 $\theta$ 去极大化 $\ell(\theta)$ 的下界。
假设 $\theta^{(t)}$是第$t$次迭代后的参数值,那么,一般的EM算法的步骤如下所示:
循环重复直至收敛 {
E Step: 对于每个 $i$, 计算: \(Q\left(z^{(i)}\right)=p\left(z^{(i)} \mid x^{(i)} ; \theta^{(t)}\right)\) M Step: 计算 \(\begin{aligned} \theta^{(t+1)} &= \arg \max _{\theta} \sum_{i=1}^{m} \sum_{z^{(i)}} Q\left(z^{(i)}\right) \log \frac{p\left(x^{(i)}, z^{(i)} ; \theta\right)}{Q\left(z^{(i)}\right)} \\ &= \arg \max _{\theta} \sum_{i=1}^{m} \sum_{z^{(i)}} Q\left(z^{(i)}\right) \log p\left(x^{(i)}, z^{(i)} ; \theta\right) - \sum_{i=1}^{m} \sum_{z^{(i)}} Q\left(z^{(i)}\right) \log Q\left(z^{(i)}\right) \end{aligned}\) 其中最后一项是常数,对于求最大似然估计,并没什么卵用,因此去掉。 \(\theta^{(t+1)} = \arg \max _{\theta} \sum_{i=1}^{m} \sum_{z^{(i)}} Q\left(z^{(i)}\right) \log p\left(x^{(i)}, z^{(i)} ; \theta\right)\) }
在2.1小节末尾的时候我们提到了,如果直接求导来最大化 $\ell(\theta)$ 的话,log里面还有多个+号,将导致无法求解。现在,通过E步我们巧妙的为 $\ell(\theta)$ 构建了一个下界。其实我们可以把这个下界理解为 $\ell(\theta)$ 的新的表达形式。这个新的表达形式能够很容易的进行求导,因为log里面的+号都被去掉了。
2.4. 证明收敛
设第 $t$ 次迭代后,$Q_{i}^{(t)}\left(z^{(i)}\right)=p\left(z^{(i)} \mid x^{(i)} ; \theta^{(t)}\right)$ , 则我们有以下式子成立: \(\begin{aligned} \ell\left(\theta^{(t+1)}\right) & \geq \sum_{i=1}^{m} \sum_{z^{(i)}} Q^{(t)}\left(z^{(i)}\right) \log \frac{p\left(x^{(i)}, z^{(i)} ; \theta^{(t+1)}\right)}{Q^{(t)}\left(z^{(i)}\right)} \\ & \geq \sum_{i=1}^{m} \sum_{z^{(i)}} Q^{(t)}\left(z^{(i)}\right) \log \frac{p\left(x^{(i)}, z^{(i)} ; \theta^{(t)}\right)}{Q^{(t)}\left(z^{(t)}\right)} \\ &=\ell\left(\theta^{(t)}\right) \end{aligned}\) 解释:
-
根据Jensen不等式,第一行的不等式对于任意 $Q$ 成立。
-
第一行到第二行是因为: \(\theta^{(t+1)}=\arg \max _{\theta} \sum_{i=1}^{m} \sum_{z^{(i)}} Q^{(t)}\left(z^{(i)}\right) \log \frac{p\left(x^{(i)}, z^{(i)} ; \theta^{(t)}\right)}{Q^{(t)}\left(z^{(i)}\right)}\)
-
第二行到第三行是因为 $Q^{(t)}\left(z^{(i)}\right)$ 满足了等式成立的条件。所以综上所述: $\ell\left(\theta^{(t)}\right) \leq \ell\left(\theta^{(t+1)}\right)$。
-
$\ell(\theta)$ 是一个依赖于 $\theta$ 和 $z$ 的分布的一个值。在t+1次迭代时,我们需要计算 $p\left(x^{(i)}, z^{(i)} ; \theta^{(t)} \right)$。实际上,这部分计算其实是以以下形式完成的: \(p\left(x^{(i)}, z^{(i)} ; \theta^{(t)} \right) = p\left(x^{(i)}; z^{(i)},\theta^{(t)} \right) \times p\left(z^{(i)} \right)\) 其中,$p\left(z^{(i)} \right)$ 就是 $z$ 的先验概率分布。在迭代更新的过程中,其实这个先验就是第t次(
这里绝对没写错)迭代中E步所算的后验概率(或者想GMM一样做一下变形,使得所有样本的 $z$ 先验都一样),可以认为是个常数。最开始的迭代,我们一般会假设一个 $z$ 的先验分布 (样本属于各类的概率均衡)。
2.5. 直观解释整个EM的过程
- EM算法解决的问题是含有隐藏变量 $z$ 的多状态或者多模型参数优化问题。其中 $z$ 表示的是某个样本属于某个类别或者模型。
- 由于 $z$ 是隐藏变量,也可以认为是缺失值,我们是不知道 $z$ 的,我们只能通过历史数据有个 $z$ 的先验概率分布。
- EM之所以叫期望最大值算法,其实就是因为E Step用期望值 $Q\left(z^{(i)}\right)$ 去替代未知的 $z$ , 然后再基于这个期望做参数最优化。这个期望不是随便来的,它恰恰是基于当前 $\theta$ 和 $x$ 值的后验概率。而这个后验概率好神奇的有很好的数学性质可以让 $\ell(\theta)$ 去掉 log 里面的连加符号从而有了一个易于求导的新的表达形式。
- 整个过程可以这么理解:我们不知道 $z$ -> 通过历史数据得到 $z$ 的先验概率 -> 根据当前参数和样本值得到后验概率,也就是更加有可能的 $z$ 的分布 -> 这个后验概率让 $\ell(\theta)$ 有了新的易于求导的形式 ,这也就是$\ell(\theta)$的下限 -> 优化参数 -> 当前的后验概率在下一轮迭代中成为先验概率 -> 直至收敛。
3. GMM高斯混合模型
下面让我们来看高斯混合模型这个具体的例子,以便更好的理解EM算法。给定训练集 $T={x^{(1)}, x^{(2)}, \ldots, x^{(m)}}$,求生成 $T$ 的混合概率模型。我们设模型的2个变量为:$\mu_{1, \ldots, k} \text { 和 } \Sigma_{1, \ldots, k}$。其中, $\mu$ 表示单个高斯模型的均值,$\Sigma$ 表示方差。设先验概率为 $\phi$, $\phi_{j}^{(i)}$ 表示先验概率 $p\left(z^{(i)}=j\right)$,$z^{(i)}$ 的取值范围是 ${1, 2, …, k} $。因此,我们的目标似然函数为:
\(\ell(\mu, \Sigma)=\sum_{i=1}^{m} \log p\left(x^{(i)} ; \mu, \Sigma\right)=\sum_{i=1}^{m} \log \sum_{z^{(i)}=1}^{k} p\left(x^{(i)} \mid z^{(i)} ; \mu, \Sigma\right) p\left(z^{(i)} ; \phi\right)\) 显然,如果我们直接对此求导,我们会发现发现log里面有很多+号项,导致求导很困难。
3.1. 那用EM算法怎么做呢?
-
E Step:
用贝叶斯来算后验概率: \(Q\left(z^{(i)}=j\right)=p\left(z^{(i)}=j \mid x^{(i)} ; \mu, \Sigma\right)=\frac{p\left(x^{(i)} \mid z^{(i)}=j ; \mu, \Sigma\right) p\left(z^{(i)}=j ; \phi\right)}{\sum_{l=1}^{k} p\left(x^{(i)} \mid z^{(i)}=l ; \mu, \Sigma\right) p\left(z^{(i)}=l ; \phi\right)}\)
-
M Step:
-
更新下一轮的先验 \(\phi_{j}:=\frac{1}{m} \sum_{i=1}^{m} Q\left(z^{(i)}=j\right)\) 这样做也可以,这样就表示对于每个样本的先验都是一样的。
-
更新模型参数 \(\mu_{j}:=\frac{\sum_{i=1}^{m} Q\left(z^{(i)}=j\right) x^{(i)}}{\sum_{i=1}^{m} Q\left(z^{(i)}=j\right)}\)
\[\Sigma_{j}:=\frac{\sum_{i=1}^{m} Q\left(z^{(i)}=j\right)\left(x^{(i)}-\mu_{j}\right)\left(x^{(i)}-\mu_{j}\right)^{T}}{\sum_{i=1}^{m} Q\left(z^{(i)}=j\right)}\]上述2个公式是求argmax高斯模型参数的最简形式。证明过程请看下面。
-
3.2. 推倒 (部分)
- 代入相应的概率模型
- 求导,以 $\mu_l$ 为例 \(\begin{aligned} \nabla_{\mu_{l}} & \sum_{i=1}^{m} \sum_{j=1}^{k} Q\left(z^{(i)}=j\right) \log \frac{\frac{1}{(2 \pi)^{n / 2}\left|\Sigma_{j}\right|^{1 / 2}} \exp \left(-\frac{1}{2}\left(x^{(i)}-\mu_{j}\right)^{T} \Sigma_{j}^{-1}\left(x^{(i)}-\mu_{j}\right)\right) \cdot \phi_{j}}{Q\left(z^{(i)}=j\right)} \\ &=-\nabla_{\mu_{l}} \sum_{i=1}^{m} \sum_{j=1}^{k} Q\left(z^{(i)}=j\right) \frac{1}{2}\left(x^{(i)}-\mu_{j}\right)^{T} \Sigma_{j}^{-1}\left(x^{(i)}-\mu_{j}\right) \\ &=\frac{1}{2} \sum_{i=1}^{m} Q\left(z^{(i)}=l\right) \nabla_{\mu_{i}} 2 \mu_{l}^{T} \Sigma_{l}^{-1} x^{(i)}-\mu_{l}^{T} \Sigma_{l}^{-1} \mu_{l} \\ &=\sum^{m} Q\left(z^{(i)}=l\right)\left(\Sigma_{l}^{-1} x^{(i)}-\Sigma_{l}^{-1} \mu_{l}\right) \end{aligned}\)
Reference:
- https://blog.csdn.net/github_36326955/article/details/55097726