Mathematical Foundation

Notes： Jekyll 对Latex公式渲染的效果一般，这个笔记可能会存在公式渲染错误的情况。最好的阅读方式clone整个blog到本地，然后用Typora打开_post文件夹下的md源文件来阅读。

1. Functions

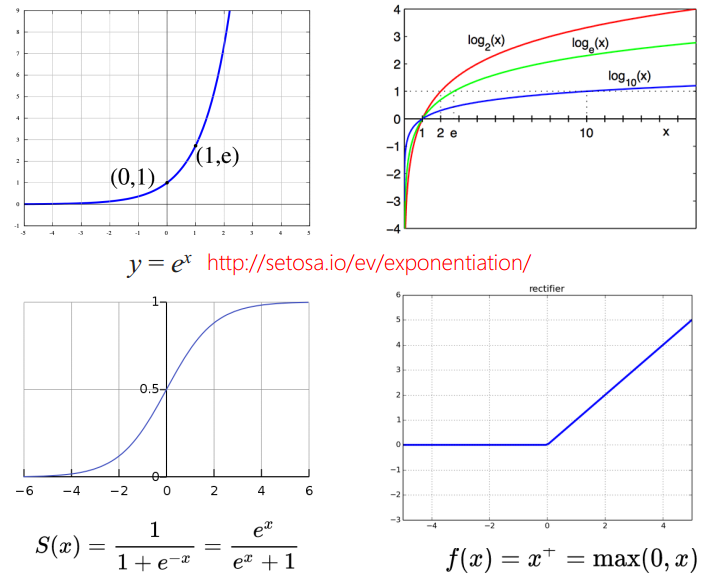
• 指数函数 $y=e^{x}$
• 对数函数 $y=log_{e}(x)$, 它和指数函数互为反函数
• Sigmoid函数 $S(x) = \frac{1}{1+e^{-x}} = \frac{e^{x}}{e^x+1}$,这个函数有特别好的数学性质，把整个实数域映射到0到1之间，经常被用作激活函数
• Rectifier $f(x) = x^+ = max(0, x)$

2. Linear Algebra

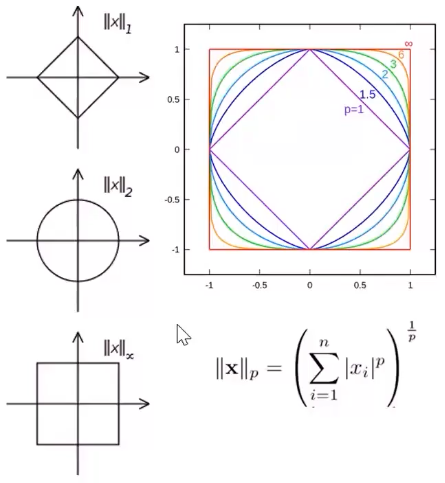
2.1. Norm of Vectors 向量的范式

向量范式用来表示向量的长度，它可以通过向量的内积来定义，在不同定义的向量内积下，向量的长度也会不同，不管其如何定义的，总满足以下几个性质：

• $\lVert x \rVert \geq 0$, with equality if and only if x = 0 (0向量)
• $\begin{equation} \lVert\alpha x \rVert=\mid \alpha \mid \lVert x \rVert \end{equation}$
• $\lVert x + y \rVert \leq \lVert x \rVert + \lVert y \rVert$ (the triangle inequality)

以下是两个常用的向量范式：

• $\ell_1$ is Manhattan Distance: $\begin{equation} \lVert x \rVert_{1} = \sum_{i=1}^{n} \mid x_{i} \mid \end{equation}$

• $\ell_2$ is Euclidean Distance: $ \lVert x \rVert_2 = \sqrt{\sum_{i=1}^{n} x_{i}^{2}}$

• 推广到general distance：$ \begin{equation} \lVert \mathbf{x} \rVert_{p} = \left( \sum_{i=1}^{n} \mid x_{i} \mid^{p} \right)^{\frac{1}{p}} \quad(p \geq 1) \end{equation}$

• 不同norm的等高线如下图所示：

  

2.2. Inner Product of Vector 向量的内积

概念

向量的内积是一个很重要的概念，它其实涵盖了向量间的距离，向量的投影，2个向量间的角度等等重要的元素。是SVM，PCA的重要理论基础。

为了更好的理解，我们先回顾一下向量的点积（dot product）: \(x\top y = \sum_{i=1}^{n} x_i y_i = \lVert x \rVert \lVert y \rVert cos\alpha\) 其中，$\alpha$是向量$x$,$y$的角度。

其中，$\alpha$是向量$x$,$y$的角度。

向量的点积其实是一种特殊的向量的内积。严格来说，向量的内积是一个很general的概念。假设$V$是向量空间，那么任何一个映射函数$\beta$，把$V \times V$映射到一个实数$R$, 而且$\beta$满足以下性质，我们就把$\beta$称之为向量的一个内积。

• 性质1 symmetric, $\beta(x, y) = \beta(y, x)$

• 性质2 positive definite, $\forall x \in V \backslash { 0 }: \beta(x, x) > 0$

• 性质3 bilinear: \(\beta(\lambda x + y, z) = \lambda \beta(x, z) + \beta(y, z)\) and \(\beta(x, \lambda y + z) = \lambda \beta(x, y) + \beta(x, z)\)

Inner Product 一般用$\langle x, y \rangle$来表示。它满足Cauchy-Schwarz不等式：

\(\lvert \langle x, y \rangle \rvert \leq \lVert x \rVert \lVert y \rVert\) 其中，$\lVert x \rVert = \sqrt{\langle x, x \rangle}$ 表示向量的长度。其实这里的向量我们是指n维空间的一个点，而向量的长度就是指这个点到原点的距离，这个距离是通过向量的内积定义的。

向量的距离

类似的，2个向量$x$和$y$的距离，也就是2个点的距离，也就是向量$x-y$的长度，我们在这里用$d(x, y)$表示： \(d(x, y) = \lVert x - y \rVert = \sqrt{\langle x - y, x - y \rangle}​\) $d(x, y)$被称为metric, 满足以下3个性质。

• positive definite $d(x, y) > 0$，当且仅当 $x = y$ 时，$d(x, y) = 0$
• symmetric $d(x, y) = d(y, x)$
• triangular inequality $d(x, z) \leq d(x, y) + d(y, z)$

向量的角度

由Cauchy-Schwarz不等式可得： \(-1 \leq \frac{\langle x, y \rangle}{\lVert x \rVert \lVert y \rVert} \leq 1\) 所以，存在一个$\omega \in [ 0, \pi ]$使得： \(cos \omega = \frac{\langle x, y \rangle}{\lVert x \rVert \lVert y \rVert}\) 这个$\omega$就是2个向量间的夹角。

如果$x \bot y$, $\langle x, y \rangle = 0$。必须要注意的一点是，我们说2个向量的垂直，是相对于在特定的内积来说的。如果是点积的话，那么垂直就是在欧式空间的垂直。

向量的投影（重要）

高维度的数据非常难以处理和分析，因此在面对高维数据的时候，我们首先要做的就是把数据进行压缩和降维，就是用更少的维度来表示数据。虽然这个压缩的过程中我们会损失数据的部分信息，但是在高维数据的众多维度当中，往往只有几个维度的信息是关键的。所以，我们必须找到最有价值的几个维度，然后把数据投影到那些维度上，然后在这些维度上进行数据分析，从而在精简数据的同时减少有效信息的损失。

我们下面来看看如何把高维向量$X \in R^n$投射到子空间$U \subseteq R^m$当中，其中$dim(U) = m$。$m$代表的是构成子空间$U$的基向量的个数。$m=1$,代表这个空间是一条直线；$m=2$,代表这个空间是一个平面；$m=3$,代表这个空间是一个三维空间，等等。

假设$P=(p_1,p_2,…,p_m)^\top$是高维子空间$U$的一组基向量，$p_i \in R^n$。$Y$是$x$在$U$上的投影，则$Y = PX$，矩阵表示如下： \(\left(\begin{array}{c} p_{1} \\ p_{2} \\ \vdots \\ p_{m} \end{array}\right)\left(\begin{array}{llll} a_{1} & a_{2} & \cdots & a_{k} \end{array}\right)=\left(\begin{array}{cccc} p_{1} a_{1} & p_{1} a_{2} & \cdots & p_{1} a_{k} \\ p_{2} a_{1} & p_{2} a_{2} & \cdots & p_{2} a_{k} \\ \vdots & \vdots & \ddots & \vdots \\ p_{m} a_{1} & p_{m} a_{2} & \cdots & p_{m} a_{k} \end{array}\right)\) 其中$p_i \in R^{n}$是一个行向量，表示子空间$U$的第$i$个基；$a_j \in R^{n}$是一个列向量，表示第$j$个原始数据记录。经过变换后，原始数据$X \in \mathbb{R}^{n * k}$从$n$维降到$Y \in \mathbb{R}^{m * k}$的$m$维。也就是说，变换后的数据维度，取决于基向量的个数。

重要结论：虽然$Y$在一个$m$维的子空间里面$U \subseteq R^m$，但是它其实是一个$n$维向量。在给定$U$的一组基向量，我们只需$P=(p_1,p_2,…,p_m)^\top$, $m$个向量，就可以近似描述一个n维向量$X$。

可以看X选择不同的基向量，我们将得到不同的数据表示。至于怎么选择这组基向量，这就是PCA要探索的东西了。

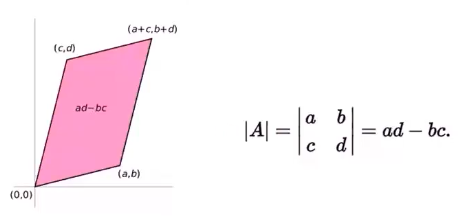
2.3. 矩阵行列式

行列式（Determinant）是数学中的一个函数，将一个 $ n\times n $的矩阵 $A$映射到一个标量，记作$ \det(A)$或 $\lvert A \rvert$。行列式可以看做是有向面积或体积的概念在一般的欧几里得空间中的推广。例如，在二维和三维空间中，行列式被解释为向量形成的图形的面积（如下图）或体积。矩阵$A = n \times n$的行列式为零当且仅当$dim(A) < n$。比如说在三维空间中，行列式为零意味着三个向量共线或者共面。

2.4. Eigenvector and Eigenvalue 特征向量和特征值

从定义出发，$Ax=\lambda x$：$A$为$n \times n$矩阵，$\lambda$为特征值，$x$为特征向量。矩阵$A$乘以$x$表示，对向量$x$进行一次转换（旋转或拉伸）（是一种线性转换），而该转换的效果为常数$\lambda$乘以向量$x$（即只进行拉伸）。

求出特征值和特征向量有什么好处呢？ 就是我们可以将矩阵$A$特征分解。如果我们求出了矩阵$A$的$n$个特征值$\lambda_1 \leq \lambda_2 \leq … \leq \lambda_n$,以及这n个特征值所对应的特征向量${w_1, w_2,…, w_n}$，如果这$n$个特征向量线性无关，那么矩阵$A$就可以用下式的特征分解表示：$A=WΣW^{−1}$。

其中$W$是这$n$个特征向量所张成的$n \times n$维矩阵，而$\Sigma$为这$n$个特征值为主对角线的n×n维矩阵。 一般我们会把$W$的这$n$个特征向量标准化，即满足$\lVert wi \rVert_2=1$, 或者说$w^\top_i w_i=1$，此时$W$的$n$个特征向量为标准正交基，满足$W^\top W=I$，即$W^\top=W^{−1}$, 也就是说W为酉矩阵。这样我们的特征分解表达式可以写成：$A=W \Sigma W^\top$。

要进行特征分解，矩阵A必须为方阵，而且A必须有n个线性无关的特征向量。那么如果A不是方阵，即行和列不相同时，我们还可以对矩阵进行分解吗？答案是可以，此时我们的SVD登场了，它可以对所有实数矩阵进行分解。

2.5. Singular Value Decomposition 奇异值分解

概述

SVD是NLP里面非常重要的一个模型。SVD也是对矩阵进行分解，但是和特征分解不同，SVD并不要求要分解的矩阵为方阵。假设我们的矩阵$A$是一个$m \times n$的矩阵，那么我们定义矩阵$A$的SVD为：$A=U \Sigma V^\top$，其中$U$是一个$m \times m$的矩阵，$\Sigma$是一个$m \times n$的矩阵，除了主对角线上的元素以外全为$0$，主对角线上的每个元素都称为奇异值，$V$是一个$n \times n$的矩阵。$U$和$V$都是酉矩阵，即满足$U^\top U=I$,$V^\top V=I$。

SVD的一些性质

对于奇异值,它跟我们特征分解中的特征值类似，在奇异值矩阵中也是按照从大到小排列，而且奇异值的减少特别的快，在很多情况下，前10%甚至1%的奇异值的和就占了全部的奇异值之和的99%以上的比例。也就是说，我们也可以用最大的k个的奇异值和对应的左右奇异向量来近似描述矩阵。也就是说： \(A_{m \times n}=U_{m \times m}\Sigma_{m \times n}V^\top_{n \times n} \approx U_{m \times k} \Sigma_{k \times k}V^\top_{k \times n}\)

其中$k$要比$n$小很多，也就是一个大的矩阵$A$可以用三个小的矩阵$U_{m \times k}$, $\Sigma_{k \times k}$, $V^\top_{k \times n}$来表示。

由于这个重要的性质，SVD可以用于PCA降维，来做数据压缩和去噪。也可以用于推荐算法，将用户和喜好对应的矩阵做特征分解，进而得到隐含的用户需求来做推荐。同时也可以用于NLP中的算法，比如潜在语义索引（LSI）。

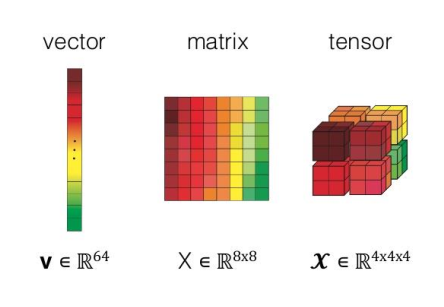
2.6. Vector to Tensor

简单来说，Tensor就是高维数组。

2.7. Jacobian and Hessian Matrices

假设$F: R_n→R_m$是一个从欧式n维空间转换到欧式m维空间的函数. 这个函数由m个实函数组成: $y_1(x_1,…,x_n), …, y_m(x_1,…,x_n)$. 这些函数的偏导数(如果存在)可以组成一个m行n列的矩阵, 这就是所谓的雅可比矩阵。 \(\mathbf{J}_{f}=\left[\begin{array}{ccc} \frac{\partial f_{1}}{\partial x_{1}} & \cdots & \frac{\partial f_{1}}{\partial x_{n}} \\ \vdots & \ddots & \vdots \\ \frac{\partial f_{m}}{\partial x_{1}} & \cdots & \frac{\partial f_{m}}{\partial x_{n}} \end{array}\right] \quad \text { i.e. } \quad\left[\mathbf{J}_{f}\right]_{i j}=\frac{\partial f_{i}}{\partial x_{j}}\)

海森矩阵(Hessian matrix或Hessian)是一个自变量为向量的实值函数的二阶偏导数组成的方块矩阵, 此函数为$f(x_1,x_2…,x_n)$。 \(\nabla^{2} f=\left[\begin{array}{ccc} \frac{\partial^{2} f}{\partial x_{1}^{2}} & \cdots & \frac{\partial^{2} f}{\partial x_{1} \partial x_{n}} \\ \vdots & \ddots & \vdots \\ \frac{\partial^{2} f}{\partial x_{n} \partial x_{1}} & \cdots & \frac{\partial^{2} f}{\partial x_{n}^{2}} \end{array}\right] \quad \text { i.e. } \quad\left[\nabla^{2} f\right]_{i j}=\frac{\partial^{2} f}{\partial x_{i} \partial x_{j}}\)

3. Convex Set and Functions

凸函数具有很好的数学性质，容易求导，容易梯度优化。如果可以判断一个函数是凸函数，那么就可以直接套用凸函数的数学性质。

3.1. 定义

A function is convex if \(f(t \mathbf{x}+(1-t) \mathbf{y}) \leq t f(\mathbf{x})+(1-t) f(\mathbf{y})\) for all $\mathbf{x}, \mathbf{y} \in \operatorname{dom} f$ and all $t \in[0,1]$。

3.2. Jenson不等式

如果$f$是凸函数，那么有 \(f(\frac{x+y}{2}) \leq \frac{f(x)+f(y)}{2}\) 这是Jensen不等式的常规形式，还可以扩展为：如果$x_1, x_2, …, x_k \in dom(f)$，$\theta_1, \theta_2, …, \theta_k \geq 0$ 而且 $\theta_1 + \theta_2 + … + \theta_k = 1$，则下式成立。

\(f(\theta_1x_1 + ... + \theta_kx_k) \leq \theta_1f(x_1) + ... + \theta_kf(x_k)\) 扩展至概率形式则为，把$\theta_1, \theta_2, …, \theta_k$看成是概率分布$p_1, p_2, …, p_k$，则有 \(f(p_1x_1 + ... + p_kx_k) \leq p_1f(x_1) + ... + p_kf(x_k)\) 写成期望形式为： \(f(Ex) \leq Ef(x)​\)

4. Probability and Statistics

概率分为2个流派，一个是主观概率另外一个客观概率。客观概率是通过大量重复采样来确定某件事的概率，比如说丢硬币得到正面的概率。主观概率是对某一个不确定性事件的度量，比如老王35岁了，他结婚了的概率是多少。机器学习里面的概率偏主观概率。

4.1. 条件概率

\[\begin{equation} P(A \mid B)=\frac{P(A \cap B)}{P(B)} \end{equation}\]

4.2. 全概率公式

\[\begin{equation} P(B)=\sum_{i} P\left(B \mid A_{i}\right) P\left(A_{i}\right) \end{equation}\]

4.3. 独立性判断

如果$P(A \cap B) = P(A)P(B)\(, 则事件A和B独立。 如果事件A和B不独立，则他们可以表达成以下形式：\)P(A \cap B) = P(A|B)P(B)\(或者\)P(A \cap B) = P(B|A)P(A)$.

4.4. Bayes‘ Rule (Fundamentally Important)

\[\begin{equation} \begin{aligned} \mathbf{P}\left(A_{i} \mid B\right) &=\frac{\mathbf{P}\left(A_{i}\right) \mathbf{P}\left(B \mid A_{i}\right)}{\mathbf{P}(B)} \\ &=\frac{\mathbf{P}\left(A_{i}\right) \mathbf{P}\left(B \mid A_{i}\right)}{\mathbf{P}\left(A_{1}\right) \mathbf{P}\left(B \mid A_{1}\right)+\cdots+\mathbf{P}\left(A_{n}\right) \mathbf{P}\left(B \mid A_{n}\right)} \end{aligned} \end{equation}\]

• $\mathbf{P}\left(A_{i}\right)$ 是prior，先验概率
• $\mathbf{P}\left(B \mid A_{i}\right)$ 是likelihood，似然值
• $\mathbf{P}(B)$是evidence，其实就是一个归一化因子
• 从机器学习的角度去理解：$A$其实可以理解为hypothesis，比如说一个样本属于哪一类，$B$理解为观测数据。

一个贝叶斯例子

张某为了解自己患上了X疾病的可能性，去医院作常规血液检查。其结果居然为阳性，他赶忙到网上查询。根据网上的资料，血液检查实验是有误差的，这种实验有“1%的假阳性率和1%的假阴性率”（真的患病者得到阴性结果称为假阴性，未患病的人得到阳性结果称为假阳性）。即在得病的人中做实验，有1%的概率是假阴性，99％是真阳性。而在未得病的人中做实验，有1%的概率是假阳性，99％是真阴性。于是张某根据这种解释，估计他自己得了X疾病的概率为99%。张某的推理是，既然只有1%的假阳性率，那么，99%都是真阳性，那我已被感染X病的概率便应该是99%。

张某咨询了医生，医生说：“99%？哪有那么大的感染几率啊。99％是测试的准确性，不是你得病的概率。你忘了一件事：这种X疾病的正常比例是不大的，1000个人中只有一个人有X病。”

张某不放心，又做了一个尿液检查，进一步检查他患上了X疾病的可能性，其结果仍然为阳性，尿液检查的实验有“5%的假阳性率和5%的假阴性率”。

1. 张某初始计算感染X病的概率是99%，问题出在哪？
2. 张某在血液检查之后感染X病的概率是多少？
3. 张某在血液和尿液检查之后得X病的概率是多少？
4. 如果根据张某的家族遗传信息，他得X病的概率是百分之一，请问结合血液和尿液检查结果，张某得X病的概率是多少？

原文：https://blog.csdn.net/lusongno1/article/details/80156728

1. 在这个例子中，张某由于没有认识到X疾病在人群中的患病率对于自己患病率的影响，从而得出了错误的结论。

2. 那么张某在血液检查之后的患病率是多少呢？画一张图来说明问题。

   

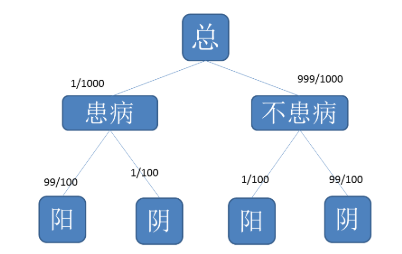
   由此，根据贝叶斯公式，可以计算张某在血液检查后患病的概率为： \(P(患/阳) = \frac{P(患)*P(阳/患)}{P(患)*P(阳/患)+P(不患)*P(阳/不患)} = \frac{99\%*1/1000}{99\%*1/1000+1\%*999/1000} \approx 9\%\)

3. 在血液检查之后，我们算得了张某患病的概率，相对于原来的1/1000，在检验血液阳性的条件下的患病的概率增加为了9%。在这样的前题之下，我们又对张某的尿液进行检查，检验为阳性。那么此时患病的概率计算方式同前，只不过是患病的概率更新为了9%。如图所示：

   

   同样地，由贝叶斯公式，有： \(P_尿(患/阳) = \frac{P_尿(患)*P_尿(阳/患)}{P_尿(患)*P_尿(阳/患)+P_尿(不患)*P_尿(阳/不患)} = \frac{95\%*9\%}{95\%*9\%+5\%*91\%} \approx 65\%\)

4. 根据张某的家族患病率，我们知道在没有任何先验信息的前题下张某的患病率为1%而不是1/1000，利用这个数值，重新进行以上的两步计算，即可知根据张某的家族遗传信息，结合血液和尿液检查结果，张某得X病的概率。计算如下： \(P(患/阳) = \frac{P(患)*P(阳/患)}{P(患)*P(阳/患)+P(不患)*P(阳/不患)} = \frac{99\%*1/100}{99\%*1/100+1\%*99/100} \approx 50\%\)

\[P_尿(患/阳) = \frac{P_尿(患)*P_尿(阳/患)}{P_尿(患)*P_尿(阳/患)+P_尿(不患)*P_尿(阳/不患)} = \frac{95\%*50\%}{95\%*50\%+5\%*50\%} \approx 95\%\]

​ 这就是说，在家族患病率和两次检查这样的前题之下，两次利用贝叶斯公式计算知张某得病的概率高达95%。

4.5. 贝叶斯学派和概率学派

a. 频率学派 - Frequentist - Maximum Likelihood Estimation (MLE，最大似然估计)

b. 贝叶斯学派 - Bayesian - Maximum A Posteriori (MAP，最大后验估计)

c. 抽象一点来讲，频率学派和贝叶斯学派对世界的认知有本质不同：频率学派认为世界是确定的，有一个本体，这个本体的真值是不变的，我们的目标就是要找到这个真值或真值所在的范围；而贝叶斯学派认为世界是不确定的，人们对世界先有一个预判，而后通过观测数据对这个预判做调整，我们的目标是要找到最优的描述这个世界的概率分布。

4.6. Random Variable 随机变量

随机变量X描述了X可能的取值的集合，比如掷骰子的可能结果为 $X \in {1,2,3,4,5,6 }$。 随机变量的完整定义包含了对每一个可能取值的概率描述，比如掷骰子的每一个结果的概率都是1/6。

• 期望：$E[X]=\sum_{x} x p(x)$
• 方差：$\operatorname{Var}(X)=E\left[(X-E[X])^{2}\right]=\sum_{x}(x-E[X])^{2} p(x)$
• 协方差：$Cov(X,Y) = E[(X-E(X))(Y-E(Y))]$表达的是X分布和Y分布的协方差。如果XY是正相关，那么它们的协方差就是一个正数，如果负相关，协方差就是一个负数。如果XY是独立的，那么它们的协方差趋向于0。

4.7. 概率符号

假设$X$是一个随机变量，$x$是它的一个实现（realization）。$\Theta$ 是一个随机变量，$\theta$是它的一个实现。

• $P(x;\beta)$（密度函数）：参数为$\beta$时$x$出现的概率。这里的$\beta$是一个参数（parameter），是一个特定的值的（注意，可能已知也可能未知）。
• $P(x \mid \theta)$（条件概率）：随机变量$\Theta$为$\theta$时，$x$出现的概率。这里$\theta$是随机变量$\Theta$的一个实现。随机变量$\Theta$是不确定的，服从一个概率分布。
• $P(x, \theta)$（联合概率）：随机变量$\Theta$为$\theta$时切随机变量$X$为$x$时的概率。

4.8. 概率密度分布函数

正态分布就是一种连续概率密度分布函数。不同的概率密度函数代表不同的概率分布的特性。在描述某些问题的时候，某些概率密度函数可能能够更贴切的反映出问题的本质。

那么学习这些概率函数有什么用呢？很多时候，我们会有观察数据，然后我们需要用一个好的概率模型或者说概率分布去描述这些数据。我们必须对常见的概率分布有所了解，才能给做出一个合理的概率模型假设。当有了一个模型假设之后，我们就能用最大似然估计去估计模型参数了。

下面是常用的几种概率密度分布函数。

1. Bernoulli Distribution (离散分布)； 最简单的0-1分布。$X \in {0,1}$, 概率密度函数为： \(f(k, p)=p^{k}(1-p)^{1-k} \quad for \quad k \in\{0,1\}\)

2. Binomial Distribution 二项式分布；每一次试验是一个Bernoulli Distribution; n次试验求k个成功那就是Binomial Distribution。注意这里k和上面k的含义不一样。概率函数为： \(f_X(n,k,p) = P(X=k) = {n \choose k}p^k (1-p)^{n-k}\)

3. Multinomial Distribution 多项式分布；Binomial Distribution单次试验只有2种结果,而Multinomial Distribution有多种结果。比如说，扔100次骰子，30次1,20次2的概率是多少。概率函数为： \(f_X(k_1,...,k_q;n;p_1,...,p_q) = P(X_1=k1;...;X_q = k_q) = \frac{n!}{x_1!...x_q!}p_1^{x_1}...p_q^{x_q}\)

4. Gamma Distribution; tend to yield skewed distributions.

5. Beta Distribution; 可以产生两头大中间小的分布。

6. Poisson Distribution；用来描述一个时间段内发生某事的次数的分布。其概率函数为($k$表示发生次数，$\lambda$表示假设概率上应该发生的次数。比如百年一遇的洪水，在100年这个时间段里，$\lambda$为1)： \(f(k,\lambda)=P(X=k)=\frac{\lambda^ke^{-\lambda}}{k!}\)

7. Gaussian Distribution; 二项式分布的极限就是正态分布。中心极限定理：给定一个任意分布的总体。每次从这些总体中随机抽取 n 个抽样，一共抽 m 次。 然后把这 m 组抽样分别求出平均值。 这些平均值的分布接近正态分布。中心极限定理使得正态分布成为最常用的分布。如果对一个分布没有任何信息，可以先假设为正态分布。

\[f(x|\mu, \sigma^2) = \frac{1}{\sqrt{2\pi \sigma^2}}e^{-\frac{(x-\mu)^2}{2\sigma^2}}\]

Reference

1. 秦曾昌 - 自然语言处理算法精讲 - Chapter 2