NLP-学习之路-5

2020-11-16

Word Representation

1. Naïve representation (One-hot):

用one-hot向量来表示，这个向量的维度是 $R^{\mid V \mid}$。也就是词袋模型。

缺点：

  1. 维度过大且sparse，大部分是0

  2. 互相垂直，用点积来计算向量距离会有问题，相同词汇的距离为1，不同词汇的距离永远为0

  3. 没有语义上的区别，比如说无法单纯从向量上体现2个词是相似的，这其实和第2点有关。

2. Count-based representation:

理论基础：

Distributional semantics, a word’s meaning is given by the words that frequently appear close-by.

方法：

  1. 考虑目标词汇的上下文，利用窗口来圈出目标词上下文，假设目标词的个数为 $\mid V \mid$。
  2. 假设所有窗口上下文里面出现过的不同的词数为 $\mid D \mid$，那么每个目标词可以表示为一个长度为 $\mid D \mid$的向量，向量的每个位置对应着上下文出现过的词，每个位置的值为该词在目标词所有的上下文出现的次数。

缺点：

  1. 每个feature都有同等的重要性，不符合真实情况

3. TF-IDF (全称：Term Frequency - Inverse Document Frequency)

TF-IDF用来衡量一个词的重要性，用来做词的特征选择，也常用于挖掘文章中的关键词，它由两部分组成：TF和IDF。

TF 词频： 指的是某一个给定的词语在该文件中出现的次数。这个数字通常会被归一化(一般是词频除以文章总词数), 以防止它偏向长的文件。

IDF 逆文档频率：log（语料库的文档总数/包含该词的文档数）

重要性：TF * IDF

缺点：

  1. 因为是词袋模型，所以没有考虑词的位置信息，出现位置靠前的词与出现位置靠后的词，都被视为重要性相同，这是不正确的。一种解决方法是，对全文的第一段和每一段的第一句话，给予较大的权重。
  2. 无法体现词在上下文的重要性。

4. Embedding Learning

Embedding Learning说白了就是要学习词的向量表达：embedding matrix。

其实上面提到的count-based的方法也产生了一个 维度为 $R^{\mid V \mid \times \mid D \mid}$ 的embedding matrix。这种embedding matrix也称为Distributional Representation，是2种主流 word representation 方法的一种。另外一种是Distributed Representation，也就是这一小节的重点。

2种representation的特点：

  1. Distributional Representation：使用词语的上下文来表示其语义，Word2vec和基于计数的词向量表示都属于这种。
  2. Distributed Representation：每个词并非采用离散的表征方式，而是被表征为一个连续的，低维，稠密的向量。与之相反的是one-hot向量。

4.1. Embedding + One-hot

假设一个词库的embedding matrix为 $E$，维度为$R^{\mid V \mid \times \mid D \mid}$。再假设词库的one-hot向量为 $O$，维度为 $R^{\mid V \mid \times 1}$。

那么一个词的向量可以由 $O^T \times E$ 获得。

4.2. 神经网络语言模型NNLM（重要节点 - 1）

这是第一个基于神经网络的语言模型，在Bengio大神在2003年发表的《A Neural Probabilistic Language Model》被提出。NNLM首次提出了word embedding的概念（虽然没有叫这个名字），从而奠定了包括word2vec在内后续研究word representation learning的基础。

NNLM的提出是为了解决N元语法模型的不足：

  1. 它无法处理更长程的context（N>3），因为长程的context出现的概率会趋向于0。
  2. 它没有考虑词与词之间内在的联系性，或者说无法建模出词之间的相似度。这是因为，N元语法本质上是将词当做一个个孤立的原子单元去处理的。这种处理方式对应到数学上的形式是一个个离散的one-hot向量。
  3. 0概率的问题。（解决这个问题有两种常用方法： 平滑法和回退法。）

NNLM：

  1. NNLM的问题设定和N元语法的目标函数一样的： \(f\left(w_{t}, w_{t-1}, \cdots, w_{t-n+1}\right)=P\left(w_{t} \mid \text { context }\right)=P\left(w_{t} \mid w_{t-1}, \cdots, w_{t-n+1}\right)\)

  2. 仔细观察能发现 $1 / P\left(w_{t} \mid w_{t-1}, \cdots, w_{t-n+1}\right)$ 其实就是单个词的困惑度perplexity。 P越大，交叉熵和困惑度都越小。

  3. NNLM的训练集：一个单词序列 $w_1, …, w_T$ （其实就是一个语料库）， 其中的每个词 $w_t \in V$，$V$ 表示一个有限的大词汇表。在N元语法中，其实训练集也是一样的，只不过是它不需要显式地去训练，而是在测试集中把需要算概率的每个词返回到训练集中数数就好了。

  4. NNLM需要满足的限制：

    1. $\sum_{i=1}^{\mid V \mid} f\left(i, w_{t-1}, \cdots, w_{t-n+1}\right)=1$
    2. $f > 0 $

    一个softmax其实就满足了。

  5. 模型结构如下图。

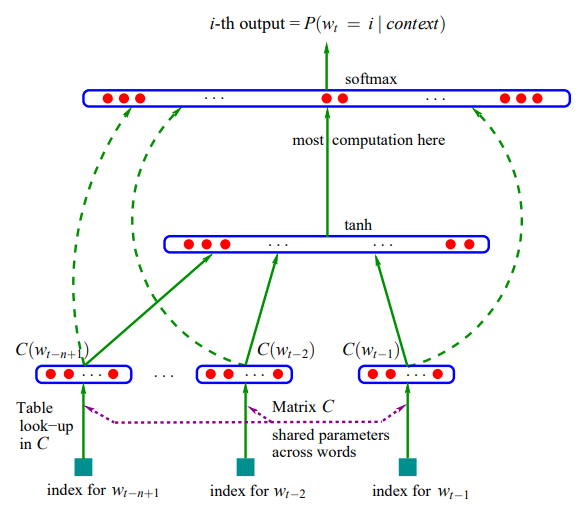
    image-20201117170304904

    整个模型可以分为2部分来理解：

    1. 首先是一个线性的Embedding层。它将输入的N−1个one-hot词向量，通过一个共享的 $D \times V$ 的矩阵 $C$，映射为 $N−1$ 个distributed词向量。其中，$C$矩阵就是要学习的distributed embedding matrix。$V$是词典的大小，$D$是Embedding向量的维度（一个先验参数）。

    2. 其次是个简单的前向反馈神经网络 $g$，对词典中的word在输入context下的条件概率做出预估： \(g\left(w_{t}, C(w_{t-1}), \cdots, C(w_{t-n+1})\right) = f\left(w_{t}, w_{t-1}, \cdots, w_{t-n+1}\right)=P\left(w_{t} \mid \text { context }\right)\) 其中，$C(w_{i})$表示词的embedding向量表示。也就是说，$g$ 的输入是 N-1 个embedding向量，$\text{input size} = (N-1) \times D$。假设隐含层有 $H$ 个单元，输入层到隐含层之间的权重矩阵的维度为 $H \times (N-1) \times D$，每个映射到隐含层的向量随后被tanh函数激活。隐含层到softmax层的矩阵维度是$V \times H$。

  6. 损失函数是一个正则化的交叉熵： \(L(\theta)=\frac{1}{T} \sum_{t} \log f\left(w_{t}, w_{t-1}, \ldots, w_{t-n+1}\right)+R(\theta)\) 其中，模型的参数 $\theta$ 包括了Embedding层矩阵$C$的元素，和前向反馈神经网络模型$g$里的权重。这是一个巨大的参数空间。不过，在用SGD学习更新模型的参数时，并不是所有的参数都需要调整（例如未在输入的context中出现的词对应的词向量）。计算的瓶颈主要是在softmax层的归一化函数上（需要对词典中所有的word计算一遍条件概率）。

  7. 仔细观察这个模型就会发现，它其实在同时解决两个问题：一个是统计语言模型里关注的条件概率 $p(w_ t \mid context)$ 的计算；一个是向量空间模型里关注的词向量的表达。而这两个问题本质上并不独立。通过引入连续的词向量和平滑的概率模型，我们就可以在一个连续空间里对序列概率进行建模，从而从根本上缓解数据稀疏性和维度灾难的问题。

4.3. Word2Vec（重要节点 - 2）

首先先来看看NNLM存在的几个问题：

  1. 同N元语法一样，NNLM模型只能处理定长的序列。Bengio将模型能够一次处理的序列长度N提高到了5，虽然相比bigram和trigram已经是很大的提升，但依然缺少灵活性。
  2. NNLM的训练太慢了。

4.2小节中我们提到了，NNLM模型可以分为2部分来理解。Mikolov意识到原始的NNLM模型计算的瓶颈主要是在softmax层的归一化函数上，也就是说瓶颈在模型的第二部分。如果我们只是想得到word的连续特征向量的话，是不是可以对第二步里的神经网络模型进行简化呢？这就是Word2Vec的出发点了。

Word2Vec由2个模型组成：CBoW （Continuous Bag-of-Words Model）和 Skip-gram Model：

其中CBOW如下图左部分所示，使用围绕目标单词的其他单词（语境）作为输入，在映射层做加权处理后输出目标单词。与CBOW根据语境预测目标单词不同，Skip-gram根据当前单词预测语境，如下图右部分所示。假如我们有一个句子“There is an apple on the table”作为训练数据，CBOW的输入为（is,an,on,the），输出为apple。而Skip-gram的输入为apple，输出为（is,an,on,the）。CBOW适合于数据集较小的情况，而Skip-Gram在大型语料中表现更好。

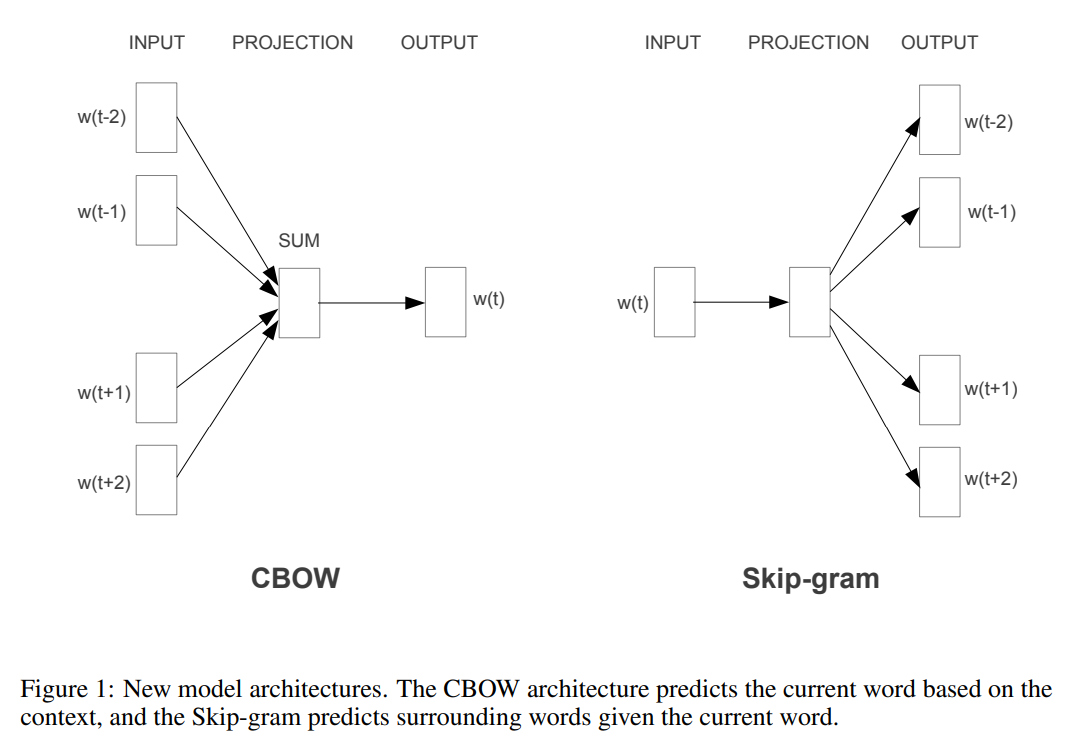
image-20201120003658435

首先来看CBoW ：

img

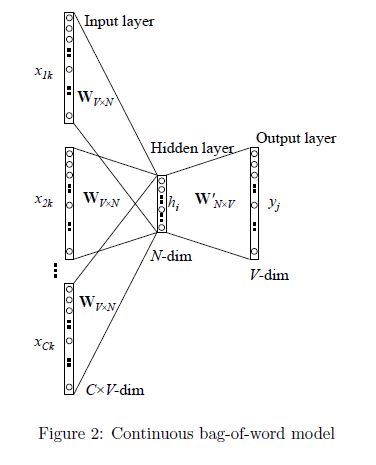
CBoW 对NNLM模型做了如下改造和简化（注意网上的这张图的notation和笔记中NNLM用到的notation不一样，对号入座即可）：

  1. 移除前向反馈神经网络中非线性的hidden layer，直接将中间层的Embedding layer与输出层的softmax layer连接；
  2. 忽略上下文环境的序列信息：输入的所有词向量均汇总到同一个Embedding layer；也就是说不再为每个输入单词维护一个embedding向量了，只维护一个：所有输入单词的embedding向量会被平均。
  3. 将Future words纳入上下文环境。

接下来是Skip-gram Model：

img

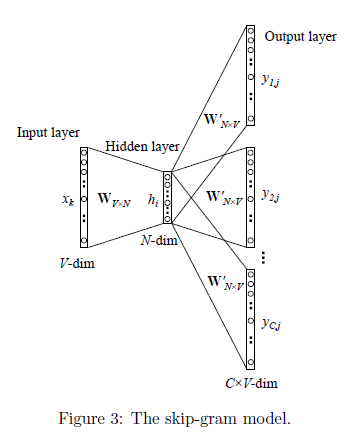
要点：

  1. 训练数据是成对出现的，如下图所示：

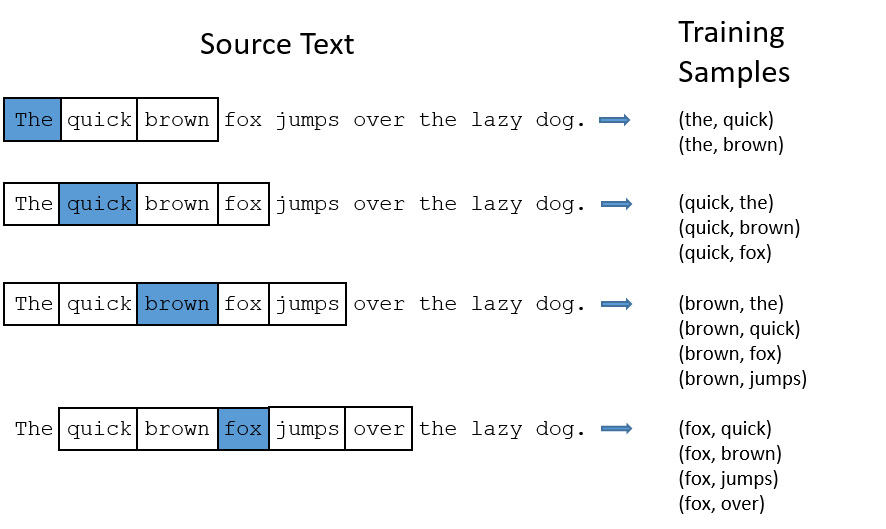
    @skip-gram的训练样本

  2. 假设训练集为：一个单词序列 $w_1, …, w_T$， 其中的每个词 $w_t \in V$，$V$ 表示一个有限的大词汇表。那么Skip-gram Model输出层的维度是 $V \times V$。

  3. 目标函数是最小化交叉熵之和： \(\frac{1}{T} \sum_{t=1}^{T} \sum_{-c \leq j \leq c, j \neq 0} \log p\left(w_{t+j} \mid w_{t}\right)\) 其中 $c$ 表示我们从中心词的一侧（左边或右边）选取词的数量，也叫做skip_window的参数。显然 $c$越大，每个词的训练数据对就越多。

4.3. Word2Vec的优化（重要节点 - 3）

然而，直接对词典里的V个词计算相似度并归一化，显然是一件极其耗时的impossible mission。为此，Mikolov引入了两种优化算法：Hierarchical Softmax 和 Negative Sampling。 （待补充）

Reference

  1. Bengio, Y., Ducharme, R., Vincent, P., & Janvin, C. (2003). A neural probabilistic language model. The Journal of Machine Learning Research, 3, 1137–1155.

    https://jmlr.org/papers/volume3/bengio03a/bengio03a.pdf

  2. Mikolov T , Chen K , Corrado G , et al. Efficient Estimation of Word Representations in Vector Space[J]. Computer Science, 2013.

    https://kopernio.com/viewer?doi=arXiv:1301.3781&route=6

  3. Mikolov T , Sutskever I , Chen K , et al. Distributed Representations of Words and Phrases and their Compositionality[J]. Advances in Neural Information Processing Systems, 2013, 26:3111-3119.

    https://papers.nips.cc/paper/2013/file/9aa42b31882ec039965f3c4923ce901b-Paper.pdf

  4. https://www.cnblogs.com/guoyaohua/p/9240336.html

  5. 秦曾昌 - 自然语言处理算法精讲 - Chapter 5