语言模型和中文分词

1. N元语法模型 (N-Gram Model)

1.1. 问题设定

猜测一个单词出现的概率。比如说有一个不完整的句子：

Please tum your homework __.

我们要猜测最有可能出现在空格的单词。

1.2. 方法：N 元语法模型

1.2.1. 定义

N 元语法模型根据前面出现的 N-1 个单词猜测接下来一个单词。一个N 元语法是包含N 个单词的序列: 2 元语法(一般称为bi-gram) 是包含2 个单词的序列，如please turn , turn your, your homework。3 元语法( 一般称为tri-gram) 是包含3 个单词的序列，如please turn your, turn your homework。计算下一个单词的概率是与计算单词序列的概率密切相关的。单词序列的概率模型又称为语言模型 (Language Models，LM)。

1.2.2. 语料库单词数目的计算

Type (型)： 语料库中不同单词的数目，或者是词汇容量的大小，记为V。在英文中需要进行词目（lemma，具有相同的词干和相同的词义并且主要的词类也相同的词汇形式）还原。

Token (例)：是使用中的全部单词数目，记为N。

1.2.3. 简单的N元语法

给定了前 n-1 个单词 $ w_1,w_2,…, w_{n-1}$，第 n 个单词为 $w_n$的概率为： \(P(x_n = w_n|x_1 = w_1, ..., x_{n-1} = w_{n-1}) = \frac{C(w_1, ..., w_n)}{C(w_1, ..., w_{n-1})}\) 其中C表示数数的意思。

好了，有了单个单词的概率之后，怎么估算整个句子的概率呢？这里假设每个单词的概率依赖于它前面的所有的单词，然后我们可以通过把若干个条件概率相乘的办法（chain rule of probability）来估计整个单词序列的联合概率。

给定单词序列：$w_1, …, w_n$，我们有： \(\begin{aligned} P\left(w_{1}, ..., w_{n}\right) &=P\left(w_{1}\right) P\left(w_{2} \mid w_{1}\right) P\left(w_{3} \mid w_{1}, w_{2}\right) \cdots P\left(w_{n} \mid w_{1}, ..., w_{n-1}\right) \\ &=\prod_{k=1}^{n} P\left(w_{k} \mid w_{1}, ..., w_{k-1}\right) \end{aligned}\)

如果单看每个词的概率，它其实就是一个N元语法，只是每个词所对应的N是不同的而已。

试想一下，随着N越来越大，其实是会出问题的，也就是，长串的词序列在语料库出现的概率会很小甚至为0，导致整个语言模型不可信。所以，在实际使用中，我们假设一个单词的概率只依赖于它前面若干个单词的概率。这种假设称为马尔可夫假设。基于这个假设，我们可以用新的概率形式来逼近上述的概率结果。比如说我们使用三元语法模型： \(\begin{aligned} P\left(w_{1}, ..., w_{n}\right) &\approx P\left(w_{1}\right) P\left(w_{2} \mid w_{1}\right) P\left(w_{3} \mid w_{1}, w_{2}\right) \cdots P\left(w_{n} \mid w_{n-2}, ..., w_{n-1}\right) \\ &=\prod_{k=1}^{n} P\left(w_{k} \mid w_{k-2}, ..., w_{k-1}\right) \end{aligned}\)

注意：

1. N 元语法模型非常依赖于训练语料库，也就是说测试语料如果和训练语料库很不同的话，测试也是没意义的。

2. 其实可以有另外一个角度去理解句子的概率，就是单个词的概率乘积，这里的 $p(x^{(i)})$ 指的是你用的语言模型下的词概率。 \(\prod_{i=1}^{n} p\left(x^{(i)}\right)\)

2. 语言模型评估 (Evaluation)：困惑度(Perplexity)

在一个测试集上语言模型的困惑度是该语言模型预测该测试集的概率的函数。对于测试集 $w=w_1, w_2, …, w_n$，困惑度就是用单词数归一化之后的测试集的概率: \(\begin{aligned} \mathrm{PP}(W) &=P\left(w_{1} w_{2} \cdots w_{N}\right)^{-\frac{1}{N}} \\ &=\sqrt[N]{\frac{1}{P\left(w_{1} w_{2} \cdots w_{N}\right)}} \end{aligned}\) 困惑度使用的单词序列就是在某个测试集中单词的整个序列。当然，由于这个序列将会跨过很多句子的边界，在计算概率时，我们有必要把句子开头和结尾的标记也包括进来。

3. 再看Cross Entropy

3.1. 语言的熵

3.1.1. 单个变量的熵

在自然语言里面，熵的计算要求我们在所要预测的范围内(单词、字母、词类，称为 $X$ 的集合)建立一个随机变 量 $X$，并且要有一个特定的概率函数称为$p(x)$，那么这个随机变量 $X$ 的熵为： \(H(X)=-\sum_{x \in X} p(x) \log _{2} p(x)\)

一般来说，熵的计算使用的log的底数是2，所以熵用比特(bit)来衡量。熵可以被想象成在最优编码中对于一定的判断或信息进行编码的比特数的下界。

来看看经典的赛马例子：假定有八匹马参加比赛，给这个消息编码的一个办法是用二进制（000， 001， …，111）代码来表示马的号码。每次比赛平均每一匹马需要用3比特来编码。但是我们可以把这件事做得更好。比如说我们可以根据赌注的实际分布来传送消息。假定每匹马的先验概率如下：

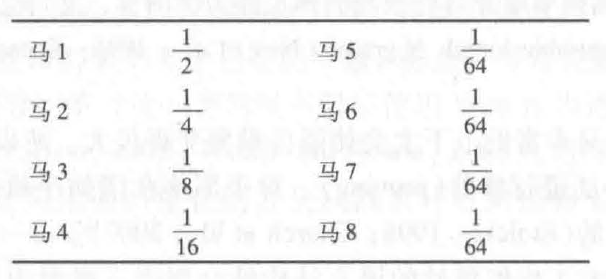
对于这些马的随机变量 $X$ 的熵可以让我们知道其比特数的下界，计算如下: \(\begin{aligned} H(X) &=-\sum_{i=1}^{i=8} p(i) \log p(i) \\ &=-\frac{1}{2} \log \frac{1}{2}-\frac{1}{4} \log \frac{1}{4}-\frac{1}{8} \log \frac{1}{8}-\frac{1}{16} \log \frac{1}{16}-4\left(\frac{1}{64} \log \frac{1}{64}\right) \\ &=2 \mathrm{bits} \end{aligned}\) 每次比赛平均为2 比特的代码可以这样来编码:用最短的代码来表示我们估计概率最大的马，估计概率越小的马，其代码越长。例如，我们可以用0来给估计概率最大的马编码，按照估计概率从大到小的排列， 其余的马的代码分别为: 10, 110, 1110, 111100, 111101, 111110, 111111。这可以看成一种数据压缩的形式。

3.1.2. 序列的熵

我们可以计算某个语言中（L）长度为 n 的单词的一切有限序列的随机变量的熵。计算公式如下: \(H\left(w_{1}, w_{2}, \cdots, w_{n}\right)=-\sum_{w_{1}, ..., w_{n} \in L} p\left(w_{1}, ..., w_{n}\right) \log p\left(w_{1}, ..., w_{n}\right)\) 每个单词的熵（per-word entropy）为用单词数来除这个序列的熵： \(H\left(w_{1}, w_{2}, \cdots, w_{n}\right)=-\frac{1}{n}\sum_{w_{1}, ..., w_{n} \in L} p\left(w_{1}, ..., w_{n}\right) \log p\left(w_{1}, ..., w_{n}\right)\) 但是为了计算一个语言的真正的俑，我们需要考虑无限长度的序列： \(\begin{aligned} H(L) &=-\lim _{n \rightarrow \infty} \frac{1}{n} H\left(w_{1}, w_{2}, \cdots, w_{n}\right) \\ &=-\lim _{n \rightarrow \infty} \frac{1}{n} \sum_{w_{1}, ..., w_{n} \in L} p\left(w_{1}, \cdots, w_{n}\right) \log p\left(w_{1}, \cdots, w_{n}\right) \end{aligned}\) Shannon -McMillian -Breiman 定理指出了，因为语言既是平稳的，又是遍历的，所以有： \(H(L)=\lim _{n \rightarrow \infty}-\frac{1}{n} \log p\left(w_{1} w_{2} \cdots w_{n}\right)\) 说了这么多其实就是为了最后这个结论。

3.2. 语言的交叉熵

假设某语言的实际概率分布为 $p$, $m$ 作为 $p$ 的一个模型。我们用 $H(p,m)$来表示交叉熵，$H(p)$来表示熵，那么显然： \(H(p) \leqslant H(p, m)\) 模型 $m$ 越精确，交叉熵就越接近于真正的熵。说白了就是交叉熵越小越好啦。好了，这时候我们上面说了这么多才得出的结论就有用了，虽然我们不知道真正的 $p$，但是我们可以给出一个近似值。在单词序列 $W$ 上， 假设我们的语言模型为 $M=P\left(w_{i} \mid w_{i-N+1} \cdots w_{i-1}\right)$，则交叉熵的近似值是： \(H(W)=-\frac{1}{N} \log P\left(w_{1} w_{2} \cdots w_{N}\right)\) 看到这里，你有没发现，其实困惑度和语言的交叉熵是有联系的！ \(\text { Perplexity }(W)=2^{H(W)}\)

4. 平滑，插值和回退

4.1. 平滑

目的：平滑是为了解决零概率的计数。

方法：

1. Laplace 平滑

   单词 $w_i$ 的非平滑的一元语法概率的最大似然度估计的计算为： \(P\left(w_{i}\right)=\frac{c}{N}\)

   其中 $c_i$ 为单词计数，$N$是用单词的”例”的总数。假设语料库有 $V$ 个不同的词，那么平滑后的概率为: \(P_{\text {Laplace }}\left(w_{i}\right)=\frac{c + 1}{N + V}\)

   在计算的时候如果想不影响分母，我们可以定义一个调整系数 $c ^ *$ ： \(c^{*}=\left(c+1\right) \frac{N}{N+V}\) 然后顺势定义一个打折系数 $d$： \(d = \frac{c^*}{c}\) 那么平滑后的概率可以看成是打折后的概率。注意，每个单词的频数都要调整，以保证所有词出现的概率总和为1。

2. Good-Turing 打折法

   虽然看起来Laplace平滑好像只是采取了统计频数+1，但是这对结果可以有很大的影响。所以这里就需要Good-Turing打折法了。Good-Turing 打折法其实就是使用只出现过一次的单词或者N元语法序列的数量作为没出现过的单词或者N元语法序列的频数来重新估计其概率的大小： \(c^{*}=(c+1) \frac{N_{c+1}}{N_{c}}\)

   \[\frac{\sum_c N_c * c^*}{N} = \frac{\sum_c(c+1) * N_{c+1}}{N} = 1\]

   其中 $N_c$表示出现次数为c次的单词（或N元序列）的数量，比如鲤鱼10 条、河鲈3 条、白鱼2 条、蹲鱼1 条、蛙鱼1 条、鲤鱼1 条，$N_1 = 3$。注意，每个单词的频数都要调整。如果 $N_{c+1} = 0$怎么办呢？这时候可以训练一个线性回归来插值： \(\log \left(N_{c}\right)=a+b \log (c)\) 显然，插值之后总的概率为不为1(应该是>1)。

   此外，在实际上，更多的是假定较大的计数是可靠的，所以我们可以引入一个阈值$k$，从而： \(c^{*}=c, \quad c>k\) 当日，引入$k$ 以后，$c^*$的计算方法也会发生相应的改变，这里就不叙述了，大概知道这个思想就可以了，用的时候可以参考 《Speech and Language Processing》 Chapter 4.

4.2. 插值和回退

除了平滑，我们还可以用插值和回退来解决零频率N 元语法的问题。以三元语法为例，在回退时，如果有非零的三元语法计数，那么，我们就仅仅依靠这些三元语法计数。只是当阶数较高的N 元语法中存在零计数的时候，我们才回退到阶数较低的N 元语法中。与此不同，在插值时，我们总是从所有的N 元语法估计中，把不同的概率估计混合起来，这就是说，我们要对三元语法、二元语法和一元语法的计数进行加权插值。

插值：

插值结合了高低元语法的优点，高元和上下文联系紧密，但稀疏，低元则相反。插值N元模型为： \(\hat{P}\left(w_{n} \mid w_{n-2} w_{n-1}\right)=\lambda_{1} P\left(w_{n} \mid w_{n-2} w_{n-1}\right)+\lambda_{2} P\left(w_{n} \mid w_{n-1}\right)+\lambda_{3} P\left(w_{n}\right)\) 其中各个 $\lambda$ 的总和为1： \(\sum_{i} \lambda_{i}=1\) $\lambda$ 的设置需要validation set。实战中可以考虑更复杂的 $\lambda$ 形式，比如说考虑上下文条件：如果对于一个特定的二元语法有特定的精确计数，我们假定基于这个二元语法的三元语法的计数非常可靠，那么我们可以使这些三元语法的 $\lambda$ 值更高，从而在插值时给三元语法更高的权值。

重要的事要不断重复： 参数设置永远是个大学问，不管什么模型，在涉及到参数设置的时候，一定要花时间去研究，去搜索，去看看人家怎么做的，结合自己的经验等等。

回退：Katz回退法。

5. 贝叶斯 & NLP

You should embrace the Bayesian approach !!!

看吧，贝叶斯真的无处不在，其实NLP里面好多任务都可以用贝叶斯来建模： \(\begin{aligned} \underset{y}{\operatorname{argmax}} P(y \mid x) &=\underset{y}{\operatorname{argmax}} \frac{P(x \mid y) P(y)}{P(x)} \\ &=\underset{y}{\operatorname{argmax}} P(x \mid y) P(y) \end{aligned}\)

现在我们来看看 $P(Y \mid X)$ 在不同场景下的含义吧，具体每个component的计算方法不是固定的，每个任务场景都不一样。而且每个任务场景都有很多都方法可以做，关键是做具体任务的时候看你怎么去理解和剖析这些子问题。

1. Spam Filtering。典型的朴素贝叶斯分类问题。X表示邮件的词序列，Y表示类别：垃圾 or not。注意需要做smoothing，大概率有些词是没在training set里面出现过的。我发现其实smoothing也可以直接给它赋个概率值就可以了，不需要考虑所有词的概率总和为1。比如说直接赋与未知词汇的概率为$P = 1/\mid V \mid$，$V$ 就是训练语料库。
2. Spelling Correction。X表示错词，Y表示潜在的正确的词。具体每个component怎么算：
   1. 在这里，先验概率P(Y)可以是个语言模型，我们需要根据前文来确定这个词出现的先验概率（我觉得）；也可以是Y的candidates里面的统计概率（视频里说的）。而在Spam Filtering中，先验的确定可以是简单的统计垃圾和非垃圾的比率。
   2. 在这个任务中，Y的candidates的确定其实是比较麻烦的，需要研究各种错词的可能性（比如说，字母被替换，缺字母，多字母，顺序调换，多种错误的混合，etc）然后反推可能正确的词，这里就不讨论了。
   3. $P(X \mid Y)$在这个任务中的计算也很tricky，需要了解每个正确的candidate词的构造规则，然后计算这个candidate到错词的概率（比如有多少个地方可插入一个字母之类的概率问题）。但是我觉得这样其实不太准，很多计算出来的概率可能会很小。还是有对应的错词语料库会更好。Anyway，每个component的建模和计算方法其实是很多的，大概了解下就可以了。
3. 语音模型。X表示语音，Y表示对应的文字。Y的candidates的确定就不讨论了。显然，P(Y)就是典型的语言模型。
4. 机器翻译。X表示语言A，Y表示语言B。同上，Y的candidates的确定就不讨论了。显然，P(Y)就是典型的语言模型。

6. 中文构词

1. 中文分词标准可以不同，没有统一的说法。
2. 分词方法：其中一种是基于词典的最大化匹配，可以从左到右，也可以从右到左，或者both。
3. 分词其实不用怎么研究了，成熟技术
4. 现成工具：Jieba for Python
5. 可以用N元语法来对分词做evaluation，比如说南京市+长江大桥的概率肯定比南京市长+江大桥的概率大。当然，训练语料库也肯定是分好词的。

Reference

1. 秦曾昌 - 自然语言处理算法精讲 - Chapter 4