NLP-学习之路-7

2020-11-22

语言技术 - 主题模型

1. 概率图模型

虽然今天用深度学习比较多，但是对于小文本、数据量不是特别大的情况，graphic model还是能提供很多有用的思路去解决问题。

其实概率图模型不是什么新东西，其实就是用图的形式来表达一个概率模型。就算是一个简单的条件概率或者是较为复杂的隐马尔科夫链模型也都可以用图来表示。图的表示方法可以让你更好的理解整个模型，比如说直观地看到变量的依赖关系啊，一个变量由什么变量决定的，那些是观测变量，那些是隐含变量等等。

2. 主题模型

在自然语言理解任务中，我们可以通过一系列的层次来提取含义——从单词、句子、段落，再到文档。在文档层面，理解文本最有效的方式之一就是分析其主题。在文档集合中学习、识别和提取这些主题的过程被称为主题建模。总的来说，主题模型可以用于文档的语义挖掘，排除文档中噪音的影响，解决多义词的问题，计算文档相似度，文本分类，推荐系统（找到相似主题的文章）等等。主题模型是语言无关的。任何语言只要能够对它进行分词，就可以进行训练（无监督），得到它的主题分布。

其实可以简单的这么理解：word2vec是用向量的形式表示词，topic model是用向量的形式表示文档。

所有主题模型都基于相同的基本假设：

  • 每个文档包含多个主题
  • 每个主题包含多个单词

换句话说，主题模型围绕着以下观点构建：实际上，文档的语义由一些我们所忽视的隐变量或「潜」变量管理。因此，主题建模的目标就是揭示这些潜在变量——也就是主题，正是它们塑造了我们文档和语料库的含义。

2.1. LSA

LSA: Latent Semantic Analysis 潜在语义分析。

算法思路：

  1. 生成文档-词语矩阵：如果在词汇表中给出 m 个文档和 n 个单词，我们可以构造一个 m×n 的矩阵 A，其中每行代表一个文档，每列代表一个单词。矩阵中的每个元素可以是该单词在对应文档的计数，也可以是单词的TF-IDF值。

  2. 问题：A 极有可能非常稀疏、噪声很大，并且在很多维度上非常冗余。解决：使用截断 SVD来降维。 \(A \approx A^{\prime} = U_{t} S_{t} V_{t}^{T}\) 直观来说，截断 SVD 可以看作只保留我们变换空间中最重要的 t 维。

    img

  3. 在这种情况下，$U \in R^{m⨉t}$是我们的文档-主题矩阵，而 $V \in R^{n⨉t}$则成为我们的词语-主题矩阵。在矩阵 U 和 V 中，每一列对应于我们 t 个主题当中的一个。在 U 中，行表示按主题表达的文档向量；在 V 中，行代表按主题表达的术语向量。

  4. 通过这些文档向量和术语向量，现在我们可以轻松应用余弦相似度等度量来评估以下指标：

    • 不同文档的相似度
    • 不同单词的相似度
    • 单词（或「queries」）与文档的相似度

LSA优点是快速且高效，但是也有主要缺点：

  1. 缺乏可解释的嵌入（我们并不知道主题是什么，其成分可能积极或消极，这一点是随机的）
  2. 需要大量的文件和词汇来获得准确的结果
  3. SVD的计算复杂度很高，而且当有新的文档来到时，若要更新模型需重新训练。（SVD做的是线性的变换）
  4. 表征效率低

2.2. PLSA

PLSA: Probabilistic Latent Semantic Analysis 概率潜在语义分析。

PLSA采取概率方法替代 SVD 以解决问题。其核心思想是找到生成文档-词语矩阵中观察到的数据的概率模型P(D,W)。PLSA有一个重要的假设就是词袋假设，即认为一篇文档中的单词是可以交换次序的而不影响模型的训练结果。

回想一下主题模型的基本假设：每个文档由多个主题组成，每个主题由多个单词组成。PLSA 为这些假设增加了概率自旋：

  • 给定文档 d，主题 z 以 $P(z \mid d)$ 的概率出现在该文档中

  • 给定主题 z，单词 w 以 $P(w \mid z)$ 的概率从主题 z 中提取出来

    img

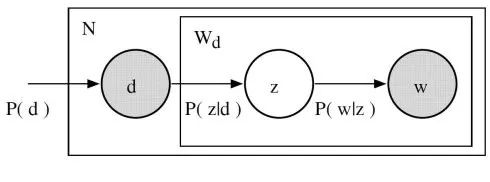
所以，从形式上来看，一个给定的文档和单词同时出现的联合概率是： \(P(d_i, w_j)=P(d_i) \sum_{z} P(z \mid d_i) P(w_j \mid z)\) 其中，$P(d_i)$ 可以直接由我们的语料库确定。$P(z \mid d_i)$ 和 $P(w_j \mid z)$ 利用了多项式分布建模。

我们可以通过极大似然来建立PLSA的目标函数： \(L=\prod_{i=1}^{N} \prod_{j=1}^{M} P\left(d_{i}, w_{j}\right)=\prod_{i} \prod_{j} P\left(d_{i}, w_{j}\right)^{n\left(d_{i}, w_{j}\right)}\) 其中 $n\left(d_{i}, w_{j}\right)$ 表示 $w_j$ 在文档 $d_i$ 中出现的次数。对目标函数两边取对数得： \(log \ L=\sum_{i} \sum_{j} n\left(d_{i}, w_{j}\right) \log \left[\sum_{k=1}^{K} P\left(w_{j} \mid z_{k}\right) P\left(z_{k} \mid d_{i}\right) P\left(d_{i}\right)\right]\) 从宏观上来说，$P\left(w_{j} \mid z_{k}\right)$ 和 $P\left(z_{k} \mid d_{i}\right)$ 就是我们待估计的两个参数（可以不用纠结多项式模型的具体参数 $\theta$，本质是一样的，只不过对于这个问题，宏观层面更方便，因为最后的迭代过程的更新公式就可以用类似这些宏观层面的条件概率来表示，数学真美！），也就是我们想要知道的各个文档下的主题概率分布以及各个主题下的词项概率分布。

如果我们对目标函数换个形式的话（为了更容易看出这是个典型的EM可解问题），则有： \(log \ L=\sum_{i} \sum_{j} n\left(d_{i}, w_{j}\right) \log \left[\sum_{k=1}^{K} P\left(w_{j} \mid z_{k}\right) P\left(d_{i} \mid z_{k}\right) P\left(z_{k}\right)\right]\) 可以看出，对于上面的目标函数，如果做极大似然估计，通过导数等于0的方式求出极大的参数，显然是行不通的，因为：

  1. 拥有隐变量z；
  2. log中有加法。

所以呢，我们需要利用EM算法来求解。具体求解可以参考Ref 2-3。E步求的就是 $z$ 的关于 $d_i$ 和 $w_j$ 的后验概率： \(P\left(z_{k} \mid d_{i}, w_{j}\right)=\frac{P\left(w_{j} \mid z_{k}\right) P\left(d_{i} \mid z_{k}\right)P(z_k)}{\sum_{l=1}^{K} P\left(w_{j} \mid z_{k}\right) P\left(d_{i} \mid z_{k}\right)P(z_k)}=\frac{P\left(w_{j} \mid z_{k}\right) P\left(z_{k} \mid d_{i}\right)P(d_i)}{\sum_{l=1}^{K} P\left(w_{j} \mid z_{k}\right) P\left(z_{k} \mid d_{i}\right)P(d_i)}\) M步就是最优化$log \ L$的下限： \(\sum_{i} \sum_{j} n\left(d_{i}, w_{j}\right) \sum_{k=1}^{K} P\left(z_{k} \mid d_{i}, w_{j}\right) \log \left[P\left(w_{j} \mid z_{k}\right) P\left(z_{k} \mid d_{i}\right)P(d_i)\right]\) 其中$P(d_i)$是个常数项，可以去掉。求解过程中还涉及到等式约束的求极值问题，需要使用Lagrange乘子法解决。这个到使用的时候再细究了。

PLSA缺点：

  1. 没有参数来给 P(D) 建模，所以不知道如何为新文档分配概率。必须在确定 document 的情况下才能对模型进行随机抽样。
  2. PLSA 的参数数量随着我们拥有的文档数线性增长，因此容易出现过度拟合问题。

很少会单独使用 PLSA。一般来说，当人们在寻找超出 LSA 基准性能的主题模型时，他们会转而使用 LDA 模型。LDA 是最常见的主题模型，它在 PLSA 的基础上进行了扩展，从而解决这些问题。

2.3. LDA

2.3.1. Dirichlet Distribution

设随机变量$x \in R^K$，K维的狄利克雷分布在数学上可以表示为： \(f\left(x_{1}, x_{2}, \ldots, x_{K} ; \alpha_{1}, \alpha_{2}, \ldots, \alpha_{K}\right)=\frac{\Gamma\left(\sum_{i=1}^{K} \alpha_{i}\right)}{\prod_{i=1}^{K} \Gamma\left(\alpha_{i}\right)} \prod_{i=1}^{K} x_{i}^{\alpha_{i}-1}\) 其中，$\Gamma$ 函数为是阶乘函数在实数域上的扩展和范化。也就是说，如果n为整数，那我们有： \(\Gamma(n)=(n-1) !\) 说白了 $\Gamma$ 函数就是一条把所有的这些阶乘点连起来的光滑曲线。利用 $\Gamma$ 函数，我们就可以得到非整数的阶乘。

狄利克雷分布有个特别好的性质：假设抽样样本 $x \in R^K$ ，那么有 $0 < x_i < 1$ 和 $\sum_{i=1}^{K} x_{i}=1$。有没发现，样本的这个性质不就是概率分布的性质吗？所以说，通常人们会叫狄利克雷分布为分布的分布。

可以看出，K维的狄利克雷分布就有K维的系数。看下图对系数和分布的关系有个大概的了解。比如说我们有个3维的狄利克雷分布，那么抽样的点肯定在第一行第3个子图的那个平面上（因为抽样数据各维度和为1嘛是吧）。那么狄利克雷分布的系数是怎么影响抽样数据分布的呢？看其他5个子图：颜色越深抽样概率越大。

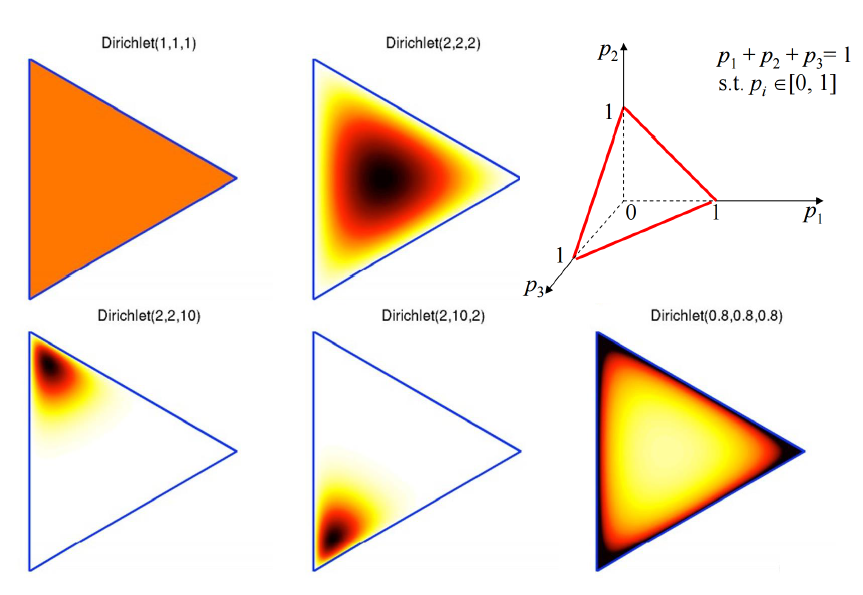
image-20201126160430101

2.3.2. 入正题

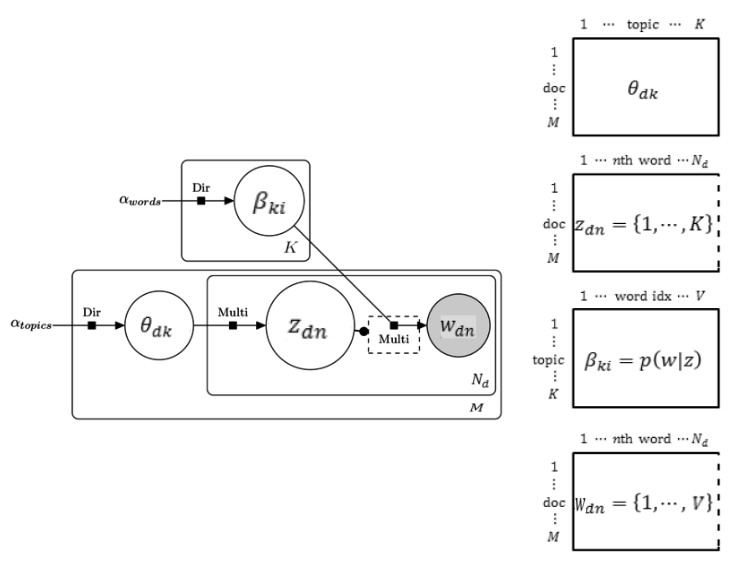
LDA的逻辑和每个参数的size和含义如下图所示。

  1. $\theta_{dk}$ （$d$ 表示文档，$k$ 表示是topic）是文档-主题矩阵，大小为 $M \times K$ ，其中 $M$ 表示文档个数，$K$ 表示topic个数。矩阵的每一行表示该文档的主题分布，服从狄利克雷分布。$\alpha_{topics}$ 是这个狄利克雷分布的参数，这个参数是$K$维的。也就是说这个主题分布由系数为$\alpha$的狄利克雷分布$Dir(\alpha_{topics})$采样得到。$\theta_{dk}$物理意义就是 $p(z \mid d)$。
  2. $z_{dn}$ （$d$ 表示文档，$n$ 表示文档的字数）是文档-字变量，大小为 $M \times N_d$，其中 $N_d$ 表示文档的字数（变长，所以 $z_{dn}$ 不是一个矩阵）。变量的每一个元素表示对应文档的对应字的主题，由关于$\theta_{dk}$的多项式分布采样得到。
  3. $\beta_{ki}$ （$k$ 表示topic，$i$ 表示字典词语）是主题-词语矩阵，大小为 $K \times \mid V \mid$ ，其中 $K$ 表示topic个数，$\mid V \mid$ 表示字典大小。矩阵的每一行表示该主题下的词语概率分布，服从狄利克雷分布。$\alpha_{words}$ 是这个狄利克雷分布的参数，这个参数是$\mid V \mid$维的。$\beta_{ki}$ 的物理意义是$p(w \mid z)$。
  4. $w_{dn}$ （$d$ 表示文档，$n$ 表示文档的字数）是文档-字变量，大小为 $M \times N_d$，其中 $N_d$ 表示文档的字数（同2，变长，所以 $w_{dn}$ 不是一个矩阵）。变量的每一个元素表示对应文档的对应字的取值（字典里面的一个字）。给定了这个字的主题（$z_{dn}$），$w_{dn}$ 由关于$\beta_{ki}$的多项式分布采样得到。

image-20201130164402746

所以LDA生成文档的流程可以总结为：

对于一篇文档d中的每一个单词，LDA根据先验知识$\alpha_{topics}$确定某篇文档的主题分布$\theta_{dk}$，然后从 $\theta_{dk}$ 所对应的多项分布中抽取一个主题z，接着根据先验知识 $\alpha_{words}$ 确定当前主题的词语分布 $\beta_{ki}$，给定主题z，然后从$\beta_{ki}$所对应的多项分布中抽取一个单词w。然后将这个过程重复$N_d$次，就产生了文档d。

事实上，理解了PLSA模型，也就差不多快理解了LDA模型，因为LDA就是在PLSA的基础上加层贝叶斯框架。LDA其实就是在PLSA的基础上给这两参数，$p(z \mid d)$ 和 $p(w \mid z)$），加了两个先验分布：一个主题分布的先验分布$Dir(\alpha_{topics})$和一个词语分布的先验分布$Dir(\alpha_{words})$。通常而言，LDA 比 PLSA 效果更好，因为它可以轻而易举地泛化到新文档中去。在 PLSA 中，文档概率是数据集中的一个固定点。如果没有看到那个文件，我们就没有那个数据点。然而，在 LDA 中，数据集作为训练数据用于文档-主题分布的狄利克雷分布。即使没有看到某个文件，我们可以很容易地从狄利克雷分布中抽样得来，并继续接下来的操作。

2.3.3. 参数估计

Gibbs采样，看看下图就好了，这里就不深究了。

image-20201130193006911

简单说说其中涉及到的一个知识点：共轭先验分布。

在贝叶斯统计中，如果后验分布与先验分布属于同类（分布形式相同），则先验分布与后验分布被称为共轭分布，而先验分布被称为似然函数的共轭先验。因为后验分布和先验分布形式相近，只是参数有所不同，这意味着当我们获得新的观察数据时，我们就能直接通过参数更新，获得新的后验分布，此后验分布将会在下次新数据到来的时候成为新的先验分布。如此一来，我们更新后验分布就不需要通过大量的计算，十分方便。

Dirichlet-Multinomial 就是一个共轭结构。在LDA中，M 篇文档会对应于 M 个独立的 Dirichlet-Multinomial 共轭结构，K 个 topic 会对应于 K 个独立的 Dirichlet-Multinomial 共轭结构。

2.3.4. 新文档主题推断

有了LDA的模型，对于新来的文档$doc_{new}$，我们如何计算它的主题分布呢？这个过程和training相似。LDA训练完之后，我们得到2个矩阵，$\theta_{dk}$和$\beta_{ki}$。其中，$\theta_{dk}$对于新文档的主题推理来说并没有用处，在工程上一般不保存。但是$\beta_{ki}$，就很有用了。在新文档的主题推断的时候，我们认为$\beta_{ki}$是不变的，是由训练语料库得到的模型提供的，所以采样过程中我们只需要估计$doc_{new}$的topic分布$\theta_{new}$就好了。

image-20201130193018107

2.4. 总结

其实，主题模型可以理解为在文档层面提取feature。所以可以把主题想象为相互垂直的feature，一个文章就是主题的线性组合。主题和词的分布概率有很大关系，比如car这个词在科技类的文档中出现的概率很高，但是在宗教类的文档中概率很低。给定一个字典$V$，不同的主题就是不同的$V$的分布。

3. 关于中文的处理

英文最小的语义单元是词，做主题模型的时候毫无疑问是基于单词来做。而中文的最小的语义单元其实是字，当然现代中文好多语义也是以词为单位了（语言在进化）。那么这里面就会存在一个问题，做主题模型的时候，是基于中文分词来做呢还是可以直接基于字来做？

秦曾昌老师做了几个实验对比了character-based LDA 和 word-based LDA：

  1. 文档生成：用训练好的LDA去生成一个文档。character-based LDA 的困惑度明显比word-based LDA低。其实这个很容易理解，因为文字的话其实就2-3千个，而这些文字组成的词就起码上万了。
  2. 文档分类：性能非常接近，但是character-based LDA 明显计算量更少。如果查看某个主题的词分布，character-based LDA的可解读性稍比word-based LDA弱，因为现代中文好多语义也是以词为单位了。
  3. 双语文档分类：双语训练集指的是，对于每一个中文文档，我们都要等价的翻译英文文档对应。在做文档分类的时候能发现，基于英文单词，中文单词，和中文字的分类结果其实很接近。

Reference

  1. https://www.jiqizhixin.com/articles/topic-modeling-with-lsa-psla-lda-and-lda2vec
  2. https://zhuanlan.zhihu.com/p/40877820
  3. https://zhuanlan.zhihu.com/p/56265390
  4. https://blog.csdn.net/github_36326955/article/details/55097726
  5. https://bloglxm.oss-cn-beijing.aliyuncs.com/lda-LDA%E6%95%B0%E5%AD%A6%E5%85%AB%E5%8D%A6.pdf
  6. 秦曾昌 - 自然语言处理算法精讲 - Chapter 7 & 8